Hash Tables from Ground Up
This post is about key-value stores and hash tables. In the first part, it will discuss how key-value stores can be implemented using arrays and binary search trees. The second part will explore the design and implementation of hash tables and discuss the different ways of resolving collisions.
Key-Value Stores
A key-value store is a type of data store that uses a key-value method to store data. Essentially, it is composed of a series of key-value pairs. A key-value pair refers to two pieces of data that are associated with each other. The key serves as a unique identifier to an associated value. Importantly, keys in a key-value store need to be unique (no duplication) in order to avoid ambiguity while searching for a specific key-value pair; the value can be any form of data, including another key-value pair.
Key-value stores are most commonly used for the following four operations:
- Inserting new key-value pairs
- Deleting existing key-value pairs
- Updating the values of existing pairs.
- Finding a value associated with a particular key. If there is no such value, then returning an exception
Key-value stores are often commonly referred to as dictionaries and associative arrays. Most programming languages have built-in versions of key-value stores. In JavaScript, for example, objects and Maps are examples of built-in key-value stores.
Direct Addressing
The simplest way to implement a key-value store is to treat the index of an array as the key and to store the associated value in the corresponding slot of the array. This works well if we can be sure that the key will always be a positive integer. Otherwise, we will need to implement a function that converts keys of other data-types to a positive integer. For example, while dealing with keys that are strings, we can use the unicode values of the constituent characters as keys. Here’s how the four key operations will be implemented:
-
Insertion: To insert a new pair (say,
kindicating the key, andvindicating the associated value), we first need to check if thekth index of the array is empty. If it is not empty, an appropriate error should be thrown as duplication of keys is not permitted. If the corresponding slot is empty, the value,v, can be inserted in thekth index. -
Deletion: To delete a key-value pair, we would just need the value of the key (
k). If thekth index of the array is empty, an appropriate error should be thrown as it would indicate an attempt to delete a pair that does not exist. Else, the value stored at thekth index should be deleted (by changing it intoundefined). The deleted value can be returned to the caller. -
Updation: To update the value of an existing key-value pair, we would need the value of the key (
k) and the new value(newVal) that needs to be updated. If thekth index is empty, an error should be thrown. Otherwise, the existing value at thekth index should be replaced by the new value (newVal). The existing value can be returned to the caller. -
Look-up: To look-up the existing value of a key-value pair, we would need the value of the key(
k). If thekth index is empty, an appropriate error should be thrown. Otherwise, the value stored at thekth index should be returned.
Here is the complete implementation of a key-value store, using arrays. (In this implementation, there is an additional method called convertToUnicode that checks if a given key is a positive integer. If it is not, it converts the key to a string, and returns the cumulative unicode values of its characters.)
While the implementation of a key-value store using an array is trivial, the time-complexity for look-up is constant. This is because of the property of arrays providing an O(1) for random access. However, it is significant to note that if we create a key-value store (phoneBook) for storing phone-numbers of persons, such that the first name of the contact acts as the key (which will first need to be appropriately converted into a positive natural number), the store will likely have a very large number of empty elements. To illustrate this, let’s use the phoneBook to store the phone numbers for two contacts, namely Bella (‘+ 91 2441139’) and Emergency (‘100’). It will first convert the names of the contacts to positive natural numbers by, say, taking the sum of the unicode values of each character of the strings. Bella will be converted to 480 and Emergency will be converted to 927. In order to store these two keys, the size of the array will be 928. In fact, if we print the contents of the array implementing the phoneBook, the output will be:
[ <480 empty items>, '+ 91 2441139', <446 empty items>, '100' ]
Arguably, the above problem arises owing to the fact that indices in an array starts with 0. In other words, if there was a way to cherry-pick the first index position of an array, the above problem could have been minimised to an extent (i.e., the array could start with 481 as the first index;but this would not be fool-proof as it would preclude insertion of keys with values less than 481) Alternatively, if we had a more efficient way to convert strings to integers, the size of the resultant array could have been reduced(i.e., if we could map Bella and Emergency to smaller positive integers). But as indices need to be arranged sequentially (preventing us from jumping indices), the potential for empty items between two values cannot be entirely eliminated. Thus, for example, if we had a key-value store that would only have even numbers as keys, the array would, at least, be twice the size of the keys actually stored.
More fundamentally, arrays become less feasible to use as key-value stores, when the set of all potential keys becomes significantly larger than the set of keys actually being stored. For example, in the case of our phone-book example, the set of ‘potential keys’ would reflect the set of every person who has a valid telephone connection (in the range of tens of millions), while the set of keys being stored, would just be the contacts (friends, families and colleagues) of the person using the phone-book (in the range of hundreds). Thus, if we assigned a unique positive natural number (starting with zero) to each person with a telephone connection, such that every phone-number (value) has an associated unique ‘key’, the key of a person (selected randomly) with a telephone connection could be anywhere between 0 and a seven digit number (assuming there to be tens of millions of telephone connections). This would mean that even if we need to store one phone-number, we may need to maintain an array of size ranging in tens of millions.
Clearly, this is a major downside of using the indices of arrays as keys for implementing associative arrays or dictionaries.
Binary Search Tree Implementation
There is a more efficient way to store key-value pairs: using binary search trees. It is an improvement over direct addressing because irrespective of the set of potential keys that can be stored, we will need to create space only for the keys actually being stored. A binary search tree allows us to keep adding new values in an orderly fashion.
Like in the case with direct addressing, this implementation will also carry out the four operations, i.e., insertion, deletion, look-up and updation. Note that, each of these operations will translate to operations on the underlying binary search tree. Thus, for example, the insertion operation will insert a new node to the binary search tree, wherein each node will carry two data items—the key (which will be used to order the binary search tree) and its associated value—and two pointers—one to the left child node and one to the right child node. Here’s how key-value stores can be implemented using binary search trees.
Significantly, the time-complexity for a look-up for this implementation would be O(log n), owing to the nature of how binary search trees are structured. Thus, while binary tree based implementation provides a more efficient space-complexity than direct addressing, it is comparatively less efficient in terms of time-complexity.
Hash tables
There is a third (and more efficient) way to implement key-value stores: hash tables. A hash table is a data-structure that is built using arrays. But unlike direct addressing, the index of an array is not directly used as a key. Instead, the hash tables use a special kind of function, called hash function, to compute the index of the array from a given key.
What is a hash function?
As shown above, direct addressing becomes impractical because we have finite space to store keys while the set of potential keys can be vast and may even be infinite. Instead of storing key k in the index k of the array, we store it in h(k), where h is the hash function and k is the key. A hash function maps an infinite set of inputs to a finite set. Given this, a hash function can be used to map any arbitrary key to an index of a given size. Effectively, a hash function computes the index of a key: for a given key, the return value of the hash function (called hash-value) provides the index of the array where the associated value should be stored.
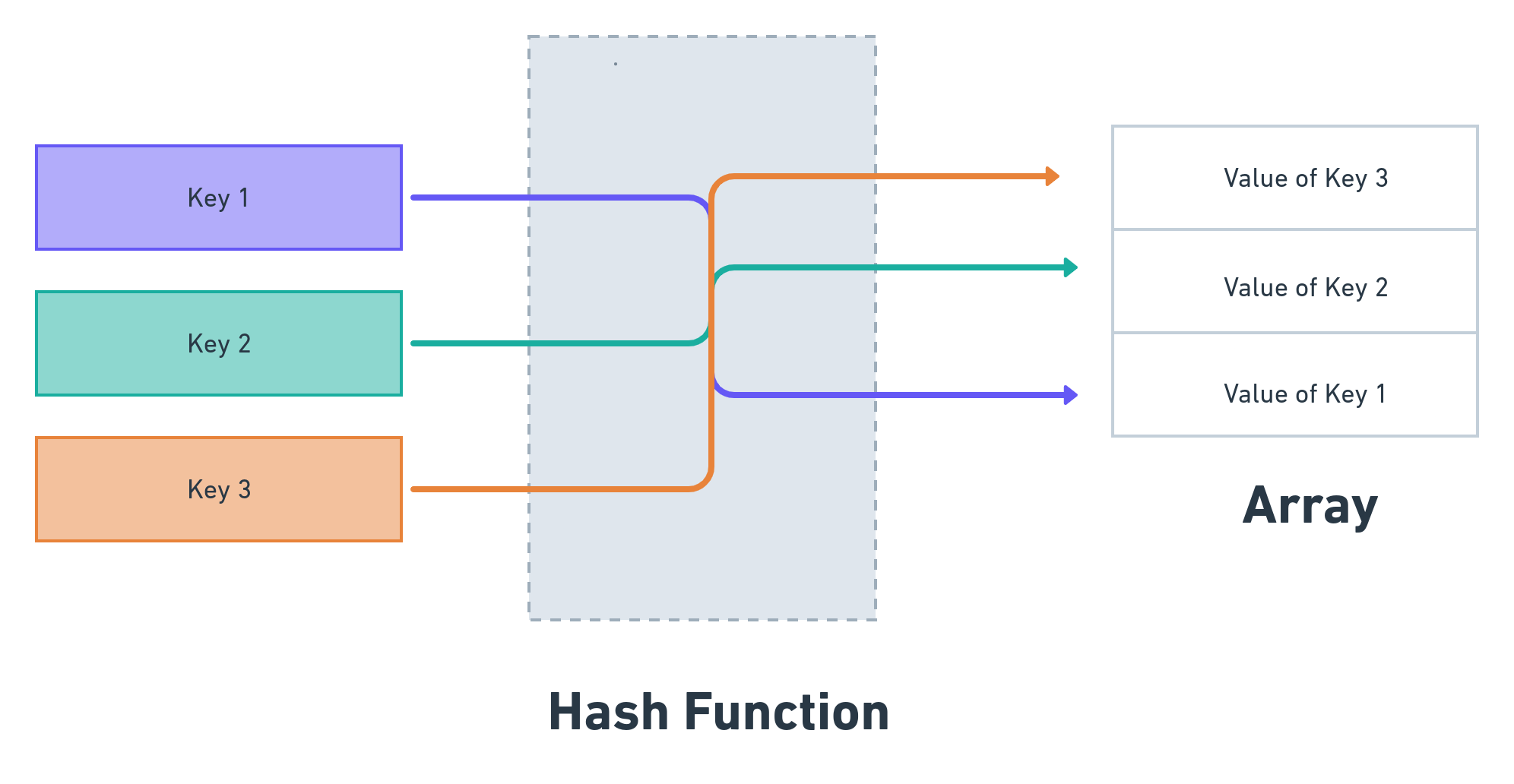
The main advantage of a hash function is that it is a many-to-one function. It maps two or more keys to a specific index of the array. This enables us to maintain an array of finite size to store keys belonging to a set of arbitrary size.
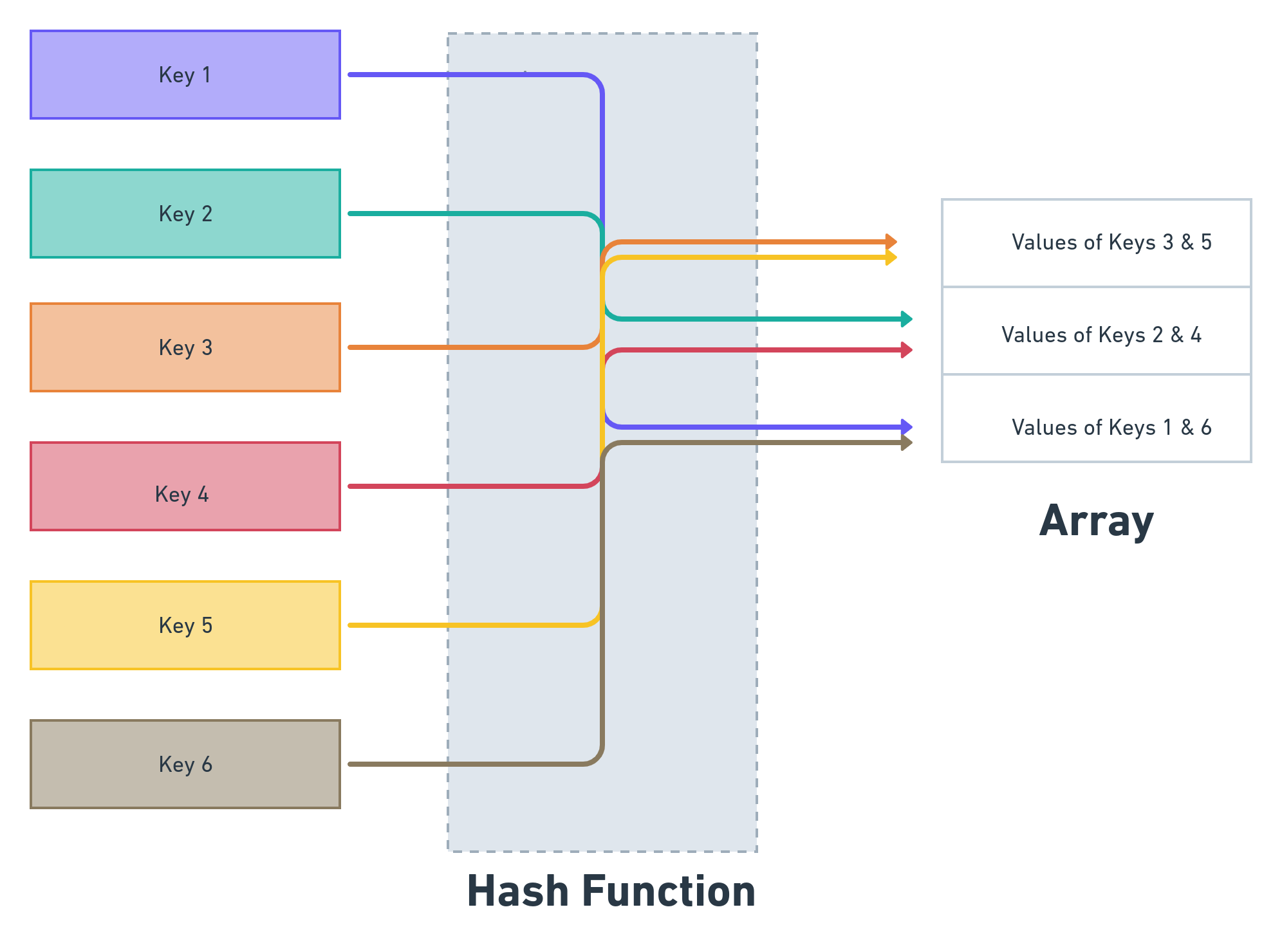
What makes a good hash function?
A good hash function is one that can satisfy the ‘simple uniform hashing’ assumption: any given key should be equally likely to be placed in any index of the array. This reduces the possibility of two keys to mapping to the same index.
However, this is difficult to achieve in practice, because it is not possible to know ex ante (i.e., at the time of designing the hash function) the nature of keys that will be passed to it. Much like the difficulty in implementing Bélády’s algorithm, it is practically not possible to predict the keys that will actually be passed to a hash function.
However, we can always rely on heuristics to reduce the possibility of such overlaps. For example, if we build a hash table to maintain a symbol-table for keywords used in the JavaScript programming language, it would be useful to ensure that the key-word let and the assignment operator (=) are not mapped to the same index, as they are often used together in a JavaScript program.
Examples of hash functions
Two common examples of hash functions: a) division method, and b) multiplication method.
Division Method
This method involves dividing a given key with the desired size of the hash table and using the remainder as the hash value.
function hashFn (k, size) => k % size;
A draw-back of this hash function is that it maps consecutive keys to consecutive hash-values, which may lead to clustering of keys (for example, if the keys are distributed in a sequential order). Generally, using prime numbers as the size of the array produces optimum results.
Multiplication Method
This method involves multiplying a given key with a constant (A), ranging between 0 and 1. The decimal part of the product is extracted by dividing it by one and using the remainder value. Finally, this is multiplied by the desired size of the array, and the rounded down value of the result is used as the hash value.
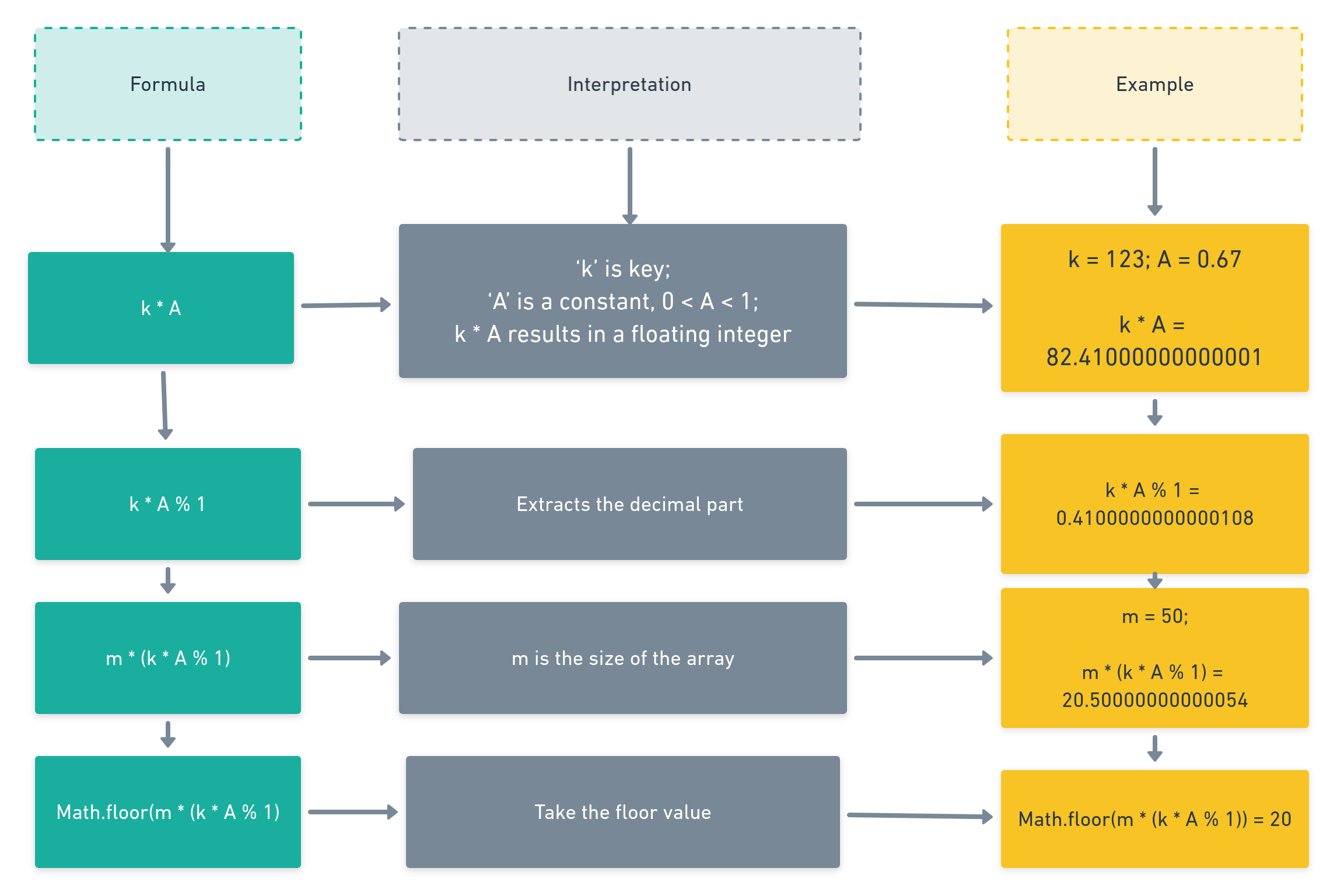
Unlike the division method, the value of m (the size of the hash table) is not crucial for the efficiency of the hash table. However, it involves more operations than the division method.
function hashFn (key) => Math.floor(m * (key * A % 1));
Hash Table: Simple implementation
Knowing how hash functions work, it is straight-forward to implement a hash table. The four operations of a key-value store can be implemented using a hash table in the following manner.
First, we need to write a class HashTable that will create the hash table. The constructor method will accept the desired size of the array of the hash table. Second, the hash function (hashFn) should be one of the methods of this class. This implementation applies the division-based hash function. Third, to ensure that, at the time of creating a hash table, all the indices of the array contain a default value (null) indicating that they are empty, the constructor should call a method (addDefaultValue) that sets all the default values of all the indices.
class HashTable {
constructor(m) {
this.arr = [];
this.size = m;
this.addDefaultValue();
}
hashFn(k) {
return k % this.size;
}
addDefaultValue(){
for(let i = 0; i < this.size; i++){
this.arr[i] = null;
}
}
Insertion
As discussed above, each key-value pair should be inserted in the index corresponding to the hash-value of the key. Thus, before carrying out the insertion, it is important to find the return value of the hash function. As our hash function will only work on positive natural numbers (as the range of hash-values should be between 0 and the desired size of the array), we need to check that first. If a given key is not a positive natural number, an appropriate error should be thrown.
Further, given that keys in a key-value store are unique (i.e., there cannot be duplicate keys in the same hash table), it will also be important to check if the given key is already a part of the hash table. If yes, an appropriate error should be thrown.
Finally, the corresponding value of the given key should be inserted at the index that is computed from the hash function. (Note that, this is a simple implementation that does not envisage collisions— handling of collisions are discussed later in this post).
insert(key, value) {
if (typeof key !== "number" || key < 0) {
throw `key is not a positive natural number ${key}`;
}
let hashValue = this.hashFn(key);
if (this.isPresent(key)) {
throw `key is already present: ${key}`;
}
this.arr[hashValue] = value;
return value;
}
Note that in the above implementation, another method (isPresent) is relied upon to check if the given key is present in the hash table. This method can be implemented by checking if there is any existing value stored in the hash-value index of the array:
isPresent(key) {
let hashValue = this.hashFn(key);
return this.arr[hashValue] != null;
}
Also, given that the other methods will also have to check if a given key is a positive natural number, it can be carried out in a separate method (isNumber), for the sake of convenience:
isNumber(key) {
return typeof key == "number" && key > 0;
}
Deletion
To carry out the deletion operation, it will be important to check: a) that the given key is a positive natural number, and b) it is currently present in the hash table. If the key is not present in the hash table or if the key is not a positive natural number, an appropriate error should be thrown.
To delete a key-value pair, the value stored in the corresponding hash-value index of the array will need to be removed (i.e., changed to null):
delete(key) {
if (this.isNumber(key)) {
let hashValue = this.hashFn(key);
if (!this.isPresent(key)) {
thorw `key is not present: ${key}`;
}
let deletedValue = this.arr[hashValue];
this.arr[hashValue] = null;
return deletedValue;
}
throw `key is not a positive natural number ${key}`;
}
Update
To implement the updation operation, the following should be checked: a) the validity of the key, and b) whether the key is present in the hash table. If the key is not present in the hash table or if the key is not valid, an appropriate error should be thrown.
To update the associated value of a key, the existing value of the hash-value index should be changed to the new value.
update(key, newVal) {
if (this.isNumber(key)) {
let hashValue = this.hashFn(key);
if (this.isPresent(key)) {
let oldVal = this.arr[hashValue];
this.arr[hashValue] = newVal;
return oldVal;
}
throw `key is not present: ${key}`;
}
throw `key is not a positive natural number ${key}`;
}
Look-up
The look-up operation should throw an error if: a) the key is not a positive natural number, or b) the key is not present in the hash table. Otherwise, it should return the value stored at the hash-value index of the array:
lookUp(key) {
if (this.isNumber(key)) {
let hashValue = this.hashFn(key);
if (this.isPresent(key)) {
return this.arr[hashValue];
}
throw `key is not present: ${key}`;
}
throw `key is not a positive natural number ${key}`;
}
Handling Collisions
Given that hash functions are many-to-one functions, it is possible that two keys that are mapped to the same slot in the array, are required to be maintained by the hash table. When this happens, there is said to be a ‘collision’.
There are largely two ways of handling collisions: a) separate chaining, and b) probing
Separate Chaining
Instead of directly storing the associated value of the key in the relevant (hash-value) index of the array, each slot of the array can contain a linked list. Each time a key-value pair needs to be inserted to the hash table, the key-value pair will be inserted as a new node in the linked list at the hash-value index of the array. In this way, in the event of a collision, additional key-value pairs will be inserted as new nodes to the relevant linked-list. This makes each index of the array, a ‘hash bucket’.
It is significant to note that, both the key and its associated value should be stored in each node of the linked list (instead of just storing the values as in the above implementation). Given that multiple keys can point to the same hash-value, it will be impossible to know which value corresponds to which key, unless we maintain the values of the key and its value in each node.
The time-complexity for the look-up operation in a linked-list is O(n). To increase the efficiency of the hash table, separate chaining can be implemented using a binary search tree (instead of a linked list), as it will provide a time-complexity of O(log n).
Implementing Separate Chaining
The following part discusses the implementation of linked-list based separate chaining.
Insertion
As opposed to the simple implementation shown above, the insertion operation should add a new node (carrying the key-value pair) to the linked-list stored in the hash-value index of the array.
insert(key, value) {
if (this.isNumber(key)) {
let hashValue = this.hashFn(key);
if (this.arr[hashValue] === null) {
this.arr[hashValue] = new Node(key, value);
return value;
}
let hashBucket = this.arr[hashValue];
if (hashBucket.find(key) === false) {
this.arr[hashValue] = hashBucket.insert(key, value);
return value;
}
throw `Key is already present in the hash bucket: ${key}`;
}
throw `Key is not a positive natural number: ${key}`;
}
The above implementation relies on an another class (Node). The constructor of this class is used to create the first node of a linked list. Thus, when the hashed-to index of the array is empty, a new instance of Node is created using the new keyword. This node is stored in that index.
class Node {
constructor(key, value) {
this.key = key;
this.value = value;
this.next = null;
}
This class contains three other methods, namely, insert, find and delete:
- insert: This method accepts a key and its value, as parameters. It inserts a new node (containing the key-value pair) to the linked-list.
- delete: This method accepts a key, and deletes the corresponding node from the linked-list containing that key.
- find: This method accepts a key, and returns the node from the linked list containing that key. If no such node exists, it returns
null
When a new key-value pair needs to be inserted to the hash table such that the hashed-to index of the array is not empty (i.e., when it contains an instance of the Node object), the insert method of that Node object is called. This method inserts a new node to the linked list and returns the (new) head node of that linked-list. The head node so returned is, then, stored in that index of the array.
insert(key, value) {
let newNode = new Node(key, value);
newNode.next = this;
return newNode;
}
delete(key) {
if (this.key === key) {
return this.next;
}
if (this.next !== null) {
this.next = this.next.delete(key);
}
return this;
}
find(key) {
if (this.key === key) {
return this;
}
if (this.next !== null) {
return this.next.find(key);
}
return null;
}
Deletion
In addition to the general checks required to be carried out (i.e., checking the validity of the key and the existence of the key in the hash table), this operation will call the delete method of the Node object stored in the relevant hashed-to index of the array. This method deletes the relevant node (containing the key) from the linked-list and returns the head node of that linked-list. The returned head node is stored in the index of the array.
delete(key) {
if (this.isNumber(key)) {
let hashVal = this.hashFn(key);
if (this.arr[hashVal] === null) {
throw `Key not present as the hash bucket is empty`;
}
let hashBucket = this.arr[hashVal];
let targetNode = hashBucket.find(key);
if (targetNode === null) {
throw `Key is not present in the hash bucket: ${key}`;
}
let deletedVal = targetNode.value;
this.arr[hashVal] = hashBucket.delete(key);
return deletedVal;
}
throw `Key is not a positive natural number: {key}`;
}
Updation and Look-Up
The updation and look-up operations will rely on the find method of the Node object stored in the hashed-to index of the array. This method returns the node containing the relevant node of the linked-list containing the given key. In the case of the updation operation, the value property of that node is updated to the new value.
update(key, newVal) {
if (this.isNumber(key)) {
let hashVal = this.hashFn(key);
if (this.arr[hashVal] === null) {
throw `Key is not present as the hash bucket is empty: ${key}`;
}
let hashBucket = this.arr[hashVal];
let targetNode = hashBucket.find(key);
if (targetNode === null) {
throw `Key is not present in the hash bucket: ${key}`;
}
let oldVal = targetNode.value;
targetNode.value = newVal;
return oldVal;
}
throw `Key is not a positive natural number: ${key}`;
}
The look-up operation works the same as update. It relies on the find method to return the value property of the targetNode. The complete implementation can be found here.
Probing
As an alternative to separate chaining, key-value pairs can be directly stored in the hash table itself. When a new pair needs to be inserted, the hashed-to slot of the hash table is examined. If it is already occupied, the next slot is examined. If that slot is also occupied, the next slot after that is examined. This continues till an empty slot is found.
The determination of the ‘next slot’ is made as per a pre-defined probing sequence. The probing sequence can be linear, quadratic etc. In a linear probing sequence, the value of the jump at each probe is fixed. For example, if the ith index is occupied, the i + 1th index will be examined and so on. In a quadratic probing sequence, each jump increments in a quadratic fashion: i, i + 1, i + 4, i + 9, i + 16…
Like in the case with separate chaining, it would be important to store both the key and its associated value in the hash table.
Also, it is important to note that while deleting an existing key-value pair from the hash table, the existing pair should be replaced with a special value (such as NaN) in order to differentiate itself from an empty slot (which is marked as null). This distinction is important, as the search for a key-value pair should be terminated only when an empty slot is reached, and not upon reaching a slot that erstwhile contained a key-value pair.
Implementing Probing
To implement the hash table operations, using linear probing, it would be crucial to write a method (findIndex) that can find the index of a given key in the hash table. This method will start from the hash-value index of the array and continue looking for the given key (by following the probing sequence), till it either reaches the given key or reaches an empty slot. If the given key is found, it should return the key-value pair. Otherwise, it should return null, indicating the absence of the key in the hash table.
In the following implementation, the findIndex method is written for a linear probing sequence:
findIndex(key) {
let hashVal = this.hashFn(key);
for (let i = hashVal; i < this.size; i++) {
if (this.arr[i] === null) {
return null;
}
if (typeof this.arr[i] === "object" && this.arr[i].key === key) {
return i;
}
}
for (let i = 0; i < hashVal; i++) {
if (this.arr[i] === null) {
return null;
}
if (typeof this.arr[i] === "object" && this.arr[i].key === key) {
return i;
}
}
return null;
}
Note that there are two for-loops: one for running the probing sequence from the hash-value index till the end of the array, and two, for running the probing sequence from the beginning of the array till the hash-value.
Insertion
A new key-value pair should be inserted in the first empty slot available, starting with the hash-value index, and following the probing sequence. As noted above, while inserting a new pair, a new object containing both the key and the value, should be inserted in the index.
insert(key, value) {
if (this.isNumber(key)) {
if (this.findIndex(key) === null) {
let hashVal = this.hashFn(key);
for (let i = hashVal; i < this.size; i++) {
if (this.arr[i] === null || Number.isNaN(this.arr[i])) {
this.arr[i] = { key: key, value: value };
return value;
}
}
for (let i = 0; i < hashVal; i++) {
if (this.arr[i] === null || Number.isNaN(this.arr[i])) {
this.arr[i] = { key: key, value: value };
return value;
}
}
throw `Hash table is full: no empty slot to add a new key-value pair. Key: ${key}`;
}
throw `Key is already present: ${key}`;
}
throw `Key is not a positive natural number: ${key}`;
}
It is important to note that, while inserting a new key-value pair, any slot containing null or NaN should be considered as an ‘empty’ slot.
Deletion
To delete an existing pair, the relevant slot of the array should be replaced with NaN:
delete(key) {
if (this.isNumber(key)) {
let targetIndex = this.findIndex(key);
if (targetIndex === null) {
throw `Key is not present in the hash table: ${key}`;
}
let oldVal = this.arr[targetIndex].value;
this.arr[targetIndex] = NaN;
return oldVal;
}
throw `Key is not a positive natural number: ${key}`;
}
Updation and LookUp
These operations are relatively straight-forward, as they mainly rely on the findIndex method to find the index of a given key.
update(key, newVal) {
if (this.isNumber(key)) {
let targetIndex = this.findIndex(key);
if (targetIndex === null) {
throw `Key is not present in the hash table: ${key}`;
}
let oldVal = this.arr[targetIndex].value;
this.arr[targetIndex].value = newVal;
return oldVal;
}
throw `Key is not a positive natural number: ${key}`;
}
lookUp(key) {
if (this.isNumber(key)) {
let targetIndex = this.findIndex(key);
if (targetIndex === null) {
throw `Key is not present in the hash table: ${key}`;
}
return this.arr[targetIndex].value;
}
throw `Key is not a positive natural number: ${key}`;
}
The complete implementation of linear probing can be found here.
Separate Chaining vs Probing
Probing is more space efficient than separate chaining, as key-value pairs are directly stored in the hash table. However, an important draw-back of probing is that it cannot be relied upon when the number of keys reaches the maximum capacity of the hash table. As key-value pairs are directly stored in the hash table, when the number of key-value pairs reach the maximum capacity, there would not be any space left in the table to insert a new pair.
On the other hand, as we use linked lists or binary search trees in separate chaining—which can store any number of nodes—there is no limitation on the total number of key-value pairs that can be stored. However, the worst-case time-complexity can become O(n) (in case of linked lists) or O(log n) (for binary search trees).
Load factor and Re-hashing
As noted above, an ideal hash function should distribute keys evenly, mainly to avoid collisions. The reason why collisions are undesirable is because it increases the time-complexity of the operations of the hash table.
In the case of separate chaining, when multiple keys get stored at the same index, the time-complexity of look-up increases: in the case of a linked list, it becomes O(n), and in case of a binary-search tree, it becomes O(log n), where ‘n’ refers to the number of keys stored in the same hash-bucket. Similarly, in the case of linear probing, the time-complexity becomes O(n), where ‘n’ refers to the number of additional indices required to be probed to reach an empty index. This significantly reduces the efficiency of a hash table, which is expected to provide constant time-complexity for look-up.
Apart from the design of the hash function, the number of keys stored in a hash-bucket vis-a-vis the total capacity of the hash table also affects the efficiency of a hash table. As the number of keys grows, the probability of collisions increases. For example, for a hash table with a capacity of 10 slots, the probability of a collision for the first key is 0, while the probability of a collision for the fifth key is 0.5. Similarly, for the tenth key, the probability of a collision is 1. This makes load factor a critical factor for determining the efficiency of a hash table.
Load factor is the ratio of the number of keys stored in a hash table to the total number of slots (or hash buckets) in the hash table. With the increase of load factor, a hash table becomes less efficient. On the other hand, a very low load factor can imply a very large number of unused hash-buckets (making it less space-efficient). As a general rule, the load-factor of 0.75 is considered an ‘ideal trade-off’ between space and time costs. However, it is important to note that in the case of separate chaining, the load factor can be greater than 1.
When the load factor of a hash table exceeds a specific value (typically 0.75), the hash table is rehashed, such that the capacity of the hash table is increased (typically, doubled in size) and the existing contents are re-mapped to the buckets of the new hash table.
Thus, to keep a track of the total number of keys stored by a hash table, the constructor should create a counter (this.keys). This counter should be increased by one, whenever a new key-value pair is inserted to the hash table. Similarly, the value of the counter should be decreased by one, when a key-value pair is deleted.
Further, the insert method of the hash table should, before inserting a new key-value pair, check if the relevant load factor of the hash table is already reached. To this end, the hash table should contain a method exceedLoadFactor to check whether the relevant load factor is reached. Finally, when the load factor is reached, a method, rehash, should be called, to double the size of the hash table.
Here’s how the insert and delete methods should be implemented (using separate chaining):
insert(key, value) {
if (this.isNumber(key)) {
//check if the size exceeds load factor
//if yes, call the method to resize
if (this.exceedLoadFactor()) {
this.rehash();
}
let hashValue = this.hashFn(key);
if (this.arr[hashValue] === null) {
this.arr[hashValue] = new hashT.Node(key, value);
this.keys++;
return value;
}
let hashBucket = this.arr[hashValue];
if (hashBucket.find(key) === null) {
this.arr[hashValue] = hashBucket.insert(key, value);
this.keys++;
return value;
}
...
}
delete(key) {
...
this.arr[hashVal] = hashBucket.delete(key);
this.keys--;
return deletedVal;
...
}
Here’s how the methods rehash and exceedLoadFactor should be implemented (the parts which are ):
rehash() {
let newSize = this.size * 2;
let newTable = new HashTable(newSize, this.load);
for (let i = 0; i < this.size; i++) {
let hashBucket = this.arr[i];
if (hashBucket !== null) {
let node = hashBucket;
while (node !== null) {
newTable.insert(node.key, node.value);
node = node.next;
}
}
}
this.size = newSize;
this.arr = newTable.arr;
}
The complete implementation can be found here.
Summary
Here’s short presentation summarising this post: