Implementing Binary Search

August 04, 2021

In this post, I write about how I solved a LeetCode problem that required implementation of binary search in a sorted array.

The problem

Given a sorted array nums containing integers and a target integer, return the index of the target in the array nums. If target is not part of the array, return the index in the array where target should be inserted.

Input: nums: [1, 3, 5, 7, 9] and target: 7
Output: 3

Input: nums: [1, 3, 5, 7, 9] and target: 6
Output: 3

Input:nums: [1, 3, 5, 7, 9] and target: 0
Output: 0

Input: nums: [1, 3, 5, 7, 9] and target: 7
Output: 5

However, the program should have a run-time complexity of O(log n).

What does O(log n) mean?

O(log n) refers to the Big-O notation. Simply put, the Big-O notation is used to loosely represent the relationship between the size of the input and the amount of time an algorithm will take to be executed. In other words, “How does the number of steps change as the input data elements increase?”.

Algorithms can have a simple and direct relationship with the input data-set: when the size of inputs increases by n, the number of operations increases by n (or, by c*n, where c is a constant). In other words, the computational time taken by such algorithms will grow proportionally to the size of the input. Such algorithms have a Big-O of n, represented as O(n).

The number of operations to be executed in an algorithm can also be independent of the size of the input data-set (e.g. finding the ith element in an array). Such algorithms have O(1), i.e., the run-time of the algorithm will be constant, and not be dependent on the input-size. (As this post is not on Big-O notation, I will reserve the discussion on Big-O for another post).

When an algorithm is said to have a O(log n), it means that the rate at which new operations (or steps) have to be carried out is a fraction of the rate at which new inputs are added. In other words, where, the input size increases by four times, but the number of additional operations only increases by two times, the algorithm will have a logarithmic time-complexity, or a O(log n).

Contrast this with algorithms with O(n), where for each increment in the input size, there is an equivalent increase in the number of operations. Or, take the case of algorithms with exponential time-complexity, which have a multiplier effect (like the rate of spread of a viral pandemic), where for n new inputs, there are c^n new operations (where, c is a constant that is greater than 1). In other words, for every increment of the input size, there is a greater corresponding increase in the time-complexity of the algorithm. As we have seen in the case of the global pandemic, exponential functions grow scarily fast. Logarithmic functions, on the other hand, can be described as inverse-exponential functions: for every n new inputs, there are less than n new set of operations. Thus, logarithmic functions grow at a very gradual pace. To illustrate this, in the following graph, the blue curve represents an exponential function (y = 2^x), the green curve represents a linear function (y = x) and the red curve represents a logarithmic function (y = log₂ n).

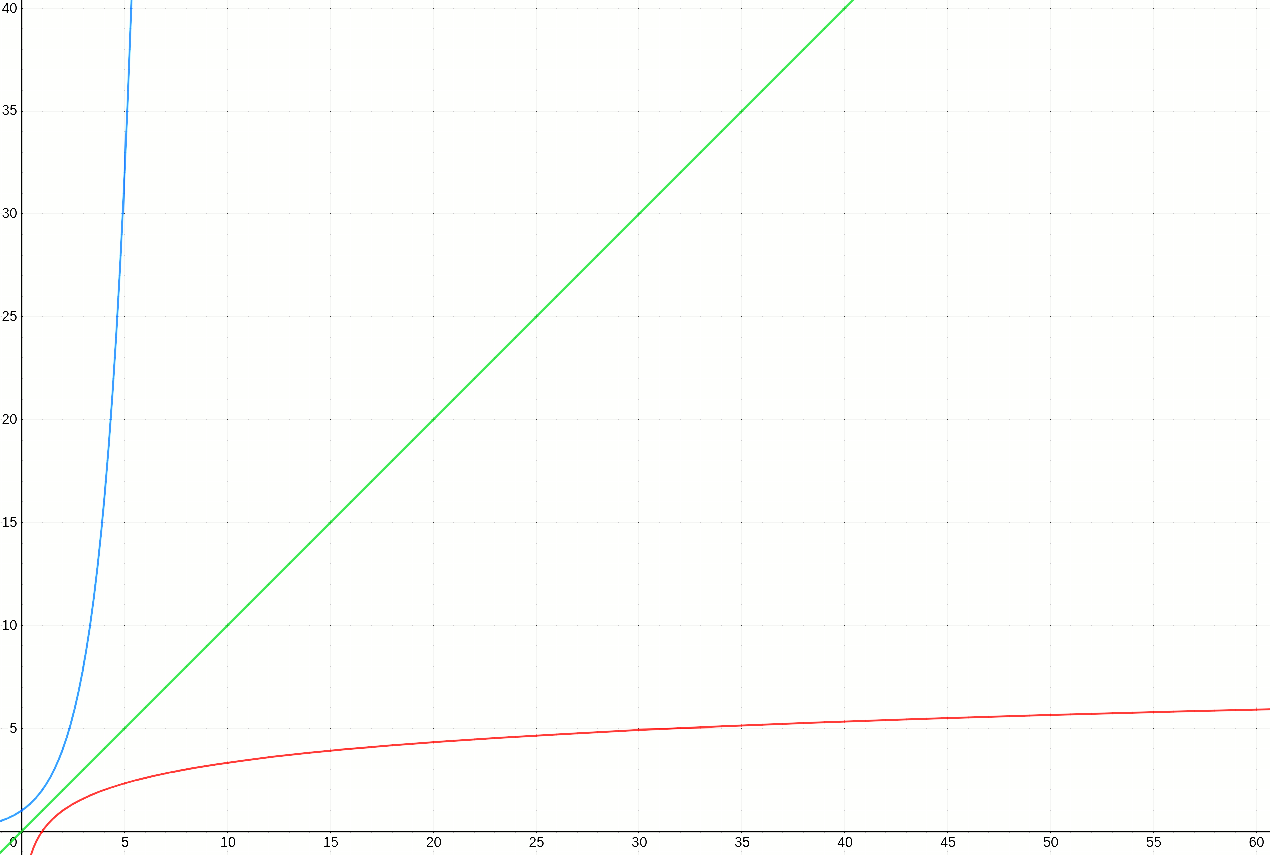
Relevance of O(log n) in the current problem

It is quite simple to write a program to find whether a target value exists in an array and to return the correct index position of the target value, if it is not present in that array:

function searchAndInsert(nums, target) {
  insertIndex = 0;
  for (let i = 0; i < nums.length; i++) {
    if (nums[i] == target) {
      return i;
    }
    if (target > nums[i]) {
      insertIndex = i + 1;
    }
  }
  return insertIndex;
}

However, this will have a time-complexity of O(n). Note that, the Big-O notation always depicts the worst-case scenario. Thus, in the above example, when the target is the last element in the array, the for-loop will run for the entire length of num. So, the number of operations is directly proportional to the input-size.

To do the same task, but with significantly fewer operations in relation to the size of the input, we cannot simply iterate through the entire array and compare each element of the array with the target value. To carry out a search that has O(log n), we will need to implement a binary search.

Binary search

What is it?

In a binary search, we start with the mid-point of the data-set (which is sorted in an ascending order). If the element in the middle of the data-set is the target value, we return the index of the middle element. Otherwise, we see if the target value is greater than or less than the value of the element in the middle. This will tell us in which half of the data-set, the target will lie. If the element in the middle of the data-set is smaller than the target, it means that target will be in the latter half (as all the elements from the 0th index till the mid-point will be smaller than the target). If the element in the middle of the data-set is greater than the target, it will mean that the target will be in the first-half of the data-set (i.e., between the 0th position and the mid-point).

During each iteration of a binary search, we divide the data-set into two halves, and then divide one of the halves into two further halves. The selection of the halves are determined by comparing the element in the middle with the target. This continues, till we reach the target, or when we are left with an empty data-set.

Here’s how to implement a binary search:

function binarySearch(nums, target) {
  let low = 0;
  let high = nums.length -1;
  let mid;
  while (low <= high) {
    mid = Math.floor((high - low) / 2) + low; //this gives us the mid-point element
    if (nums[mid] == target) {
      return mid;
    }
    //if target is greater than nums[mid], the next iteration should look at nums[mid + 1] to nums[high]
    if(target > nums[mid]){
        low = mid + 1;
    }
    //if target is less than nums[mid], the next iteration should look at nums[low] to nums[mid - 1]
    else{
        high = mid - 1;
    }
  }
  return -1; // this will signify that the target is not present in the array nums
}

In the above example, at each iteration of the while-loop, the mid-point element of the array is compared with target. If target == nums[mid], mid will be returned. Otherwise, target will be compared with nums[mid], as shown above.

There are two important points to note:

• How should values of low and high be changed during each iteration? Once we know that nums[mid] is not the target, we need not include that specific element in the next iteration. For this reason, we define low = mid + 1 when target is greater than nums[mid]. This is because, when target > nums[mid] it follows that every element in the array upto and including the element at the mid index, are less than the target and therefore, cannot contain the target. Conversely, we define high = mid - 1 when the target is less than nums[mid], because when **target < nums[mid] is less than nums[mid], it follows that every element starting with the element at mid and thereafter are greater than the target and therefore they cannot contain target**.

• When should the loop terminate? The while-loop should terminate when we are left with no more elements to look at. This is important because it can very well be the case that target is not present in nums. In the above example, we achieve this, by keeping the condition for the while-loop as low <= high. In a case where target is not present in nums, we will reach a point where both low and high are pointing to the same element in the array. At this point, the following will be true mid==low==high. Now, either the target will be less or greater than the element at the current mid index. If its the former, high will be decreased by 1. If its the latter, low will be increased by 1. In either case, it will break the condition of the while-loop as high will now be less than low.

Does binary search have an O(log n)?

While running a binary search, at each iteration, the size of the data-set shrinks by half. Assuming the worst-case scenario (i.e., when the target value is in at the index when low==high is true, i.e., when the data-set will be containing only one element), the number of elements remaining to be checked changes (at each iteration) as shown below:

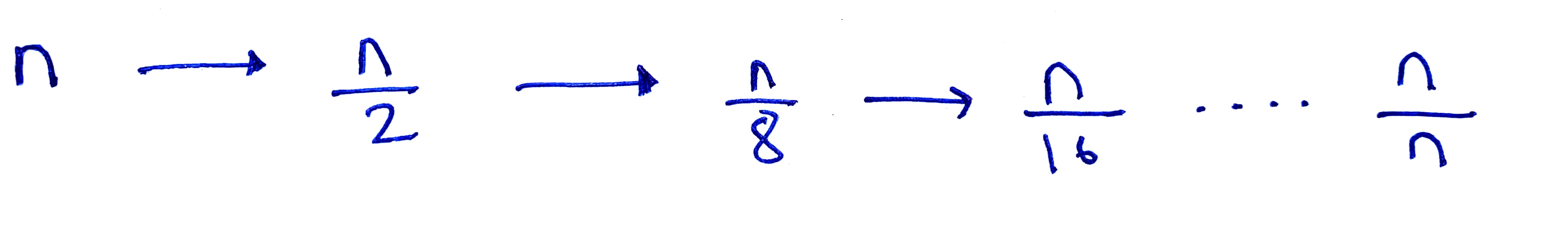
First, we have n elements to check, then by looking at the middle element of the sorted array, we throw away half the array. Now, in the selected half, we have n/2 elements, which again is halved. This continues until we have only one element remaining to be checked.

The above expression can be expressed in the following manner as well:

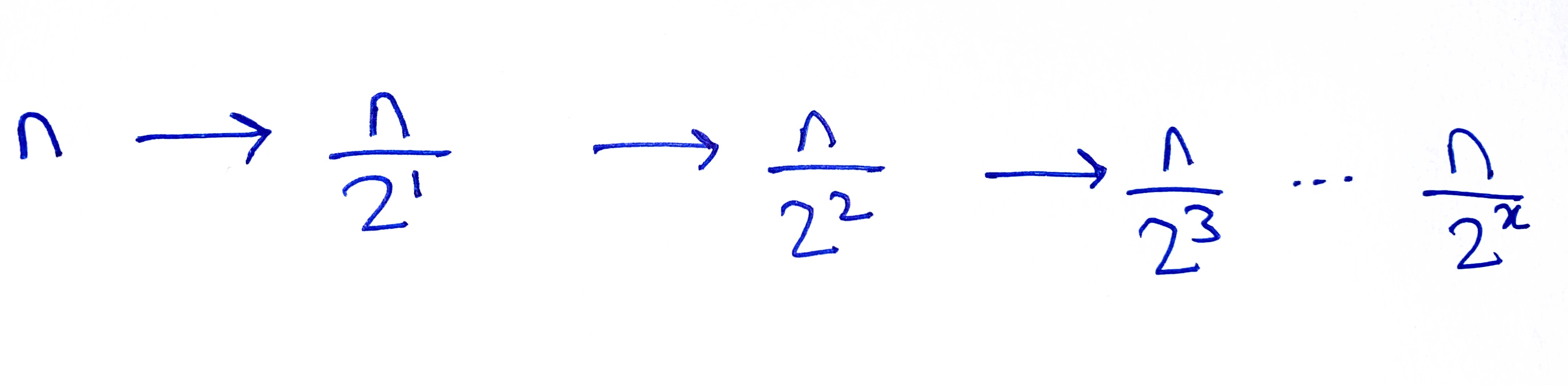
Thus, in the worst-case scenario, the total number of operations will be x:

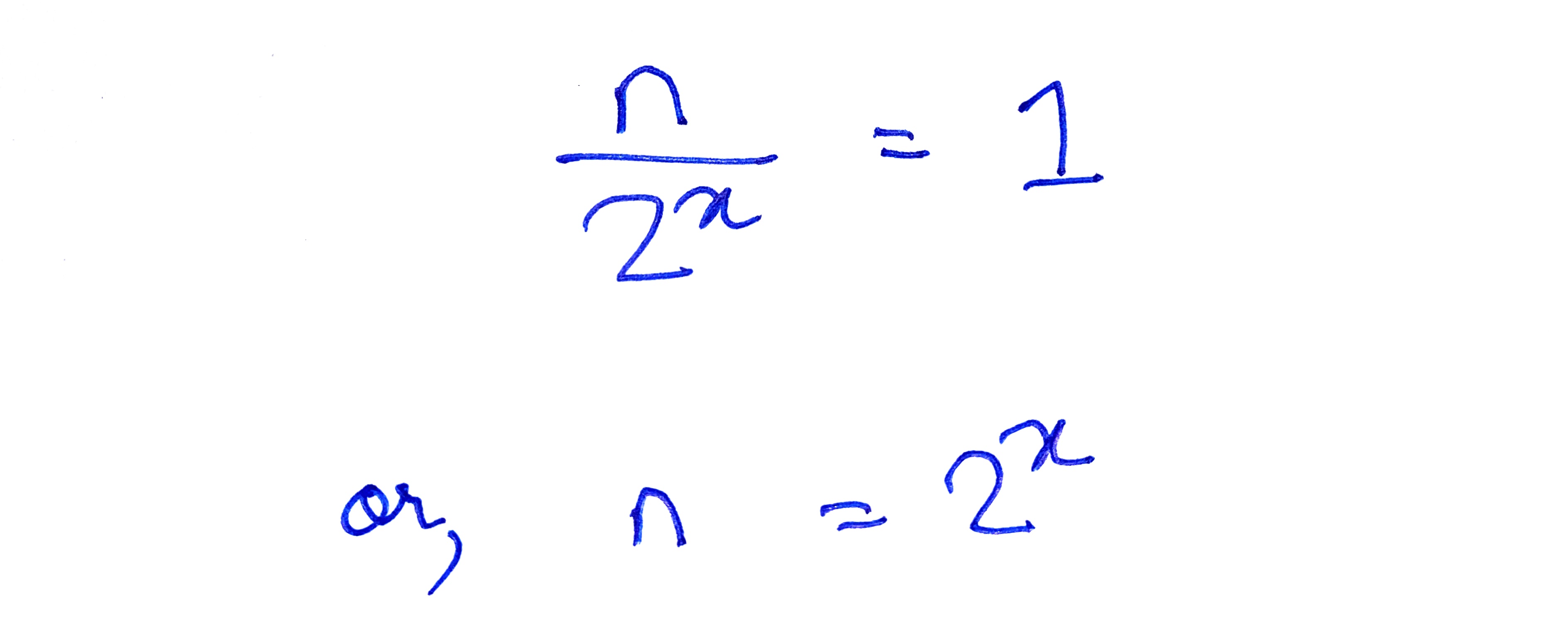
By definition, this can be expressed as:

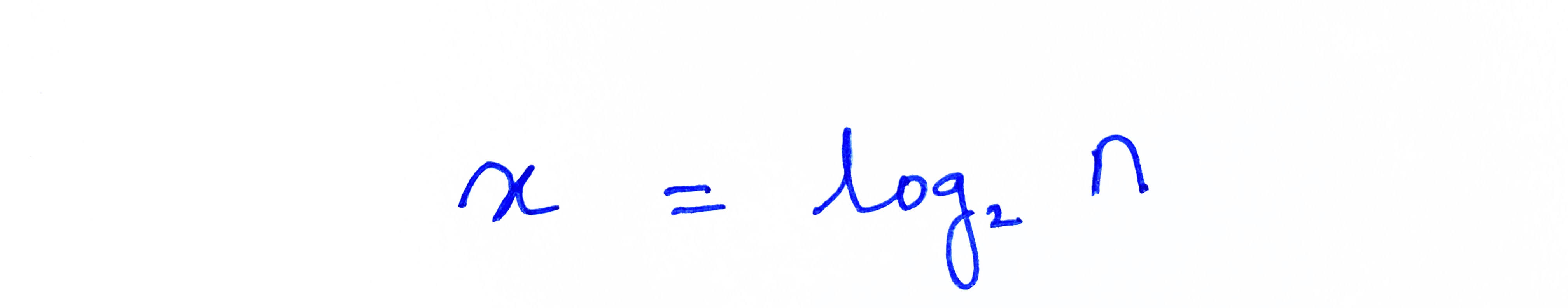
Since x represents the number of operations, the Big-O of a binary search would be: O(log n). Thus, if there were 1024 elements in an array, a linear search would require (at-most) 1024 operations to find a specific element. A binary search, on the other hand, would require only 10 steps (as log₂ 1024 = 10).

Implementing binary search and replace

The above program will not return the correct index of target if it is not present in the array (It will simply return -1 if target is not present in nums].

But the LeetCode problem at hand also requires us to accurately return the index where target should be inserted in the array nums, if it is not present already.

In the example above, when we reach the last round of the while-loop, when low==high is true, the index represented by low and high indicate the index that is nearest to where target should be present in the array.

Now, target can either be greater or less than the element at the mid/ low / high index of the array. If target < nums[mid], target should be inserted at the mid index and the element on that index should be shifted to the next index. Conversely, if target > nums[mid], target should be inserted in the index right after mid. Given this, the value of low would represent the index where target should be inserted: this is because, the value of low (which is the same value as mid in the last round of iteration), increases by 1 when target is greater than nums[mid] and the value of low remains unchanged (i.e., same as that of mid) when target is less than nums[mid]

function binarySearch(nums, target) {
  let low = 0;
  let high = nums.length -1;
  let mid;
  while (low <= high) {
    mid = Math.floor((high - low) / 2) + low; //this gives us the mid-point element
    if (nums[mid] == target) {
      return mid;
    }
    if(target > nums[mid]){
        low = mid + 1;
    }
    else{
        high = mid - 1;
    }
  }
  return low; 
}