Who Moved My Cheese: Laziness in Clojure

January 17, 2022

In this post, I try to understand what lazy sequences are and how to create our own lazy sequence in Clojure.

Lazy Sequences in Clojure

Most of the sequence library functions are lazy, i.e. functions that return seqs do so incrementally, as they are consumed, and thus consume any seq arguments incrementally as well.

The important parts of this is that many library functions that produce sequences (e.g. lists) do so incrementally, as they are consumed. This means that unless there is someone to consume the sequence, nothing really happens.

This was particularly perplexing to the eyes of a beginner learning Clojure, especially as to why the following the following does not print anything:

(defn print-numbers
  [n]
  (map println (range n)) ;; .... (1)
  (println "Done printing: " n))

When this function was called with proper arguments, the REPL produced the following output:

butterfly.core=> (print-numbers 9)
Done printing:  9
nil

It turns out that the function print-numbers produces a lazy sequence on line 1 (as indicated on the code-block above), i.e., the map produces a lazy sequence. As no one is consuming the sequence from map, it is never really realised. For this reason, the println inside the map is never executed. This is what lazy evaluation means.

This can be fixed in any of the following ways.

Using mapv

Use a non-lazy version of map, i.e., mapv

(defn print-numbers
  [n]
  (mapv println (range n))
  (println "Done printing: " n))

Using map + doall

Wrap map with doall which realises a lazy sequence

(defn print-numbers
  [n]
  (doall (map println (range n)))
  (println "Done printing: " n))

Using doseq

Instead of generating a sequence, we can use doseq which acts on each element of a sequence

(defn print-numbers
  [n]
  (doseq [i (range n)]
    (println i))
  (println "Done printing: " n))

Using run!

A better version (for the present example) than using doseq is to use run! which applies a given function on every element of a sequence, without generating another sequence (unlike map)

(defn print-numbers
  [n]
  (run! println (range n))
  (println "Done printing: " n))

Generating a Lazy Sequence 💪🏼

Let us now try to generate an infinite lazy sequence of prime numbers.

First, we write a function which returns true if a number is prime

(defn is-prime?
  [n]
  (not-any? (fn [factor]
              (zero? (mod n factor)))
            (range 2 (dec n))))

Let us now define an infinite sequence of prime numbers:

(def infinite-primes
  (filter is-prime? (drop 2 (range))))

This infinite-primes var is doing a filter operation on an infinite sequence of numbers. Because filter and range both produce lazy sequences, this will not halt our program. In fact, this is the power of lazy sequences, that we can compute as many number of prime numbers, as we need when we need it without having to know apriori how many we may need.

Thus, all of the following generates prime number sequences of varying lengths:

user=> (take 5 infinite-primes)
(2 3 5 7 11)
user=> (take 10 infinite-primes)
(2 3 5 7 11 13 17 19 23 29)
user=> (take 100 infinite-primes)
(2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541)

Constructing a Lazy Sequence from Scratch 🧙🏼

In the above part, we generated a lazy sequence by leveraging the library functions filter and range both of which are lazy.

In order to construct a lazy sequence from scratch, we can use lazy-seq. But before writing a lazy-primes function, let us write an eager-primes function that constructs a sequence of prime numbers from scratch:

(defn eager-primes
  ([n] (eager-primes n 2 []))
  ([n curr xs]
   (if (= (count xs) n)
     xs
     (if (is-prime? curr)
       (recur n (inc curr) (conj xs curr)) 
       (recur n (inc curr) xs)))))

Here’s the how eager-primes can be used:

butterfly.core=> (eager-primes 8)
[2 3 5 7 11 13 17 19]

This is not a lazy sequence, because irrespective of how many primes are consumed, eager-primes will always generate n prime numbers, no more, no less.

So, in order to make it lazy, first we need to get rid of n, so that the production of primes depends on how many are consumed and not on a pre-defined number. For example, here we need only 10 primes, but eager-primes will still generate 100 primes

(take 10 (eager-primes 100))

In order to make it a lazy sequence, we need to stop the recursion. The way to do this is to wrap the recursive call around lazy-seq. What this will do is that it will tell Clojure that if any one is consuming from this sequence, this is the step to repeat. In other words, if we have a pause/resume functionality around recur, we have essentially generated a lazy sequence. But, in practice, we cannot actually use recur because when we use lazy-seq around the recursive call, the recursive call is no longer a tail call. So, we have to make the recursive call by using the function name.

(defn primes
  ([] (primes 2))
  ([curr]
   (if (is-prime? curr)
     (cons curr (lazy-seq (primes (inc curr))))
     (lazy-seq (primes (inc curr))))))

Output:

butterfly.core=> (def all-primes (primes))
#'butterfly.core/all-primes

butterfly.core=> (take 5 all-primes )
(2 3 5 7 11)

butterfly.core=> (take 10 all-primes )
(2 3 5 7 11 13 17 19 23 29)

butterfly.core=> (take 15 all-primes )
(2 3 5 7 11 13 17 19 23 29 31 37 41 43 47)

Important things to note:

Why we must use cons: cons appends an element to a sequence at the beginning, without traversing the rest of the sequence. This is important because, if we are generating an infinite sequence, we cannot traverse the sequence fully because the sequence is infinite. In contrast, conj appends a new element at the end of the sequence, which, by definition, requires traversal of the whole sequence (to find the end). This is why we must use cons instead of conj.
Use of lazy-seq: Whenever Clojure sees lazy-seq it stops evaluation until someone is realising it. This means that a cons on a lazy sequence is a sequence which has not really been computed. It will be computed when someone is traversing that list, i.e., realising it. The way this works is that cons points to an element and a lazy sequence which, again, includes a cons cell that points to an element and another lazy sequence. The Clojure environment evaluates these lazy-seqs as demanded as the traversal progresses. Therefore, it only evaluates that part of the sequence which has been traversed at least once.

To visualize the above, let us try to understand how a lazy sequence is traversed upon realization. For example, when four elements are taken out of the lazy sequence, the following happens:

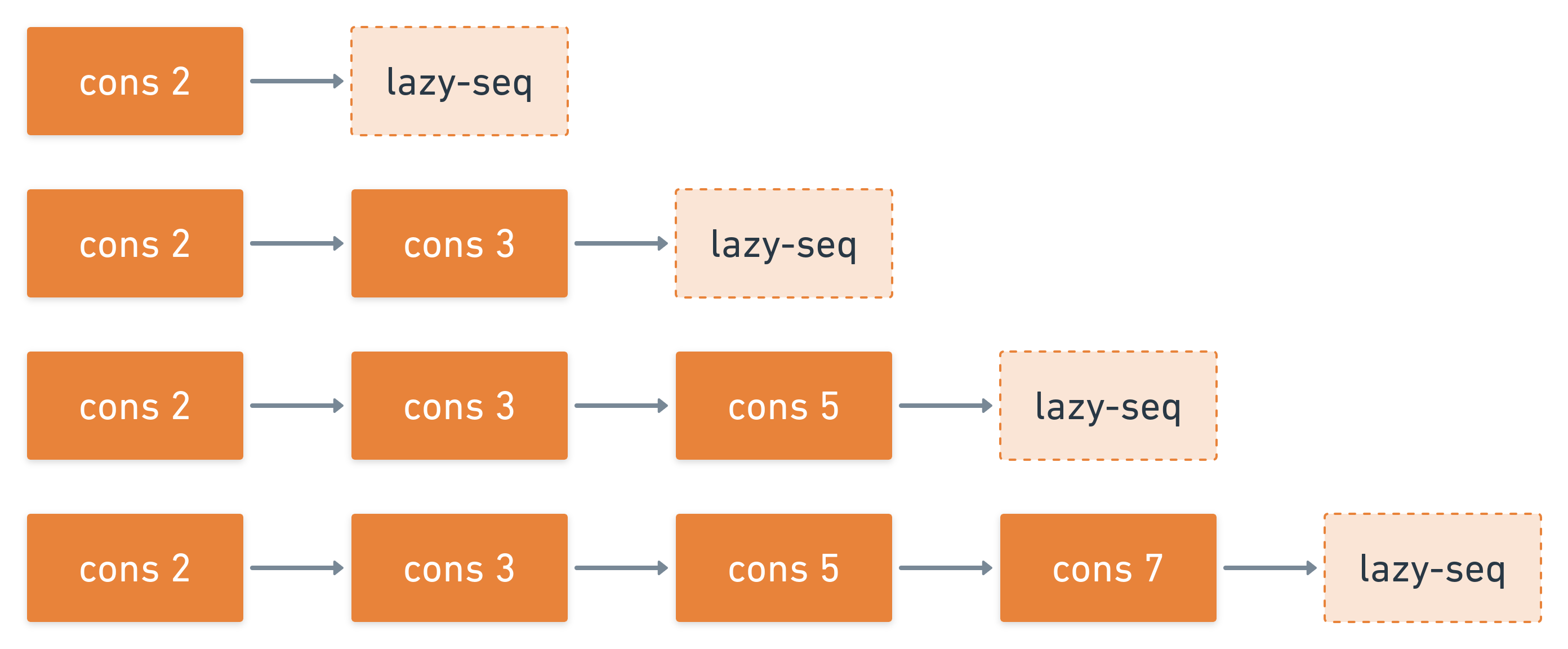
Every cons cell has a subsequent sequence, which is lazy. This means that it has not been computed. Therefore, only when we traverse that lazy sequence, do we find another cons cell with the next prime number, followed by another lazy sequence. This can be thought of as the proverbial Russian Dolls. Only by opening the first doll do you see the next doll (and not any more).

This traversal of lazy sequences and realisation (and caching of realised cons cells) is transparently done by Clojure, as they are consumed by some enclosing code. As a corollary, by virtue of the REPL having an eval step, lazy sequences are realised on the spot if directly written on the REPL (i.e., the REPL tries to consume the entire lazy sequence).

user=> (cons 1 (range))
;; this will never finish on the REPL

Who Moved My Cheese: Why laziness is not a bad thing

In the book ‘Who Moved My Cheese’, the author says that the lazy mouse ultimately loses out on life because when the going gets tough, the hard-working mouse (eager mouse) finds a solution and the lazy one, out of sheer laziness, perishes.

However, in a modern-day language like Clojure, a lazy sequence can prove to be very useful because some problems, like the prime numbers sequence, by definition, are infinite. If we built a web-page that displayed a paginated result of prime numbers, any language that did not implement a lazy sequence of prime numbers, would have to re-evaluate all the prime numbers for every page. This means that to generate the 500th prime number, we would have to generate 499 prime numbers and then the 500th one. Consequently, to generate the 501st prime number, we would have to re-generate the first 500 prime numbers all over again (as seen in the eager-primes example above). This in Clojure would not be required because we maintain only one sequence of prime numbers that are realised as required and no recomputaton would be necessary.

Edit: In an earlier version, I had mentioned that a lazy sequence can provide efficiency. This is not accurate: a lazy sequence does not improve the inherent algorithmic efficiency of an expression. (However, caching of a lazy sequence does prevent recomputations). Thanks to Aditya Athalye, for pointing this out!