Crisp: A Simple Lisp Interpreter

August 24, 2021

In this post, I discuss about building a simple Lisp interpreter, written in JavaScript, supporting basic Clojure syntax.

Infix Expressions and Operator Precedence

In arithmetic expressions, the operator is always placed in between the operands. For example, an expression to multiply 2, 3 and 4 would be written as follows: 2 * 3 * 4. Because the operator is sandwiched between operands, these expressions are also called infix expressions.

But when there are different operators in a single expression, it can result in some confusion. Take, for example, the expression, 2 * 3 + 4. If 2 and 3 are multiplied first and then 4 is added, the result would be 10. However, if 3 and 4 are added first and then multiplied by 2, the result would be 14.

To prevent this kind of confusion, there is a collection of rules, called operator precedence, that have evolved ever since the introduction of algebraic notation, that dictate the order of precedence among operators. These rules are often abbreviated as BEMDAS, to signify the order among some of the common operators: Brackets, Exponents, Multiplication, Division, Addition, and Subtraction.

Just like in arithmetic expressions, it can get equally confusing for the compiler of a programming language to evaluate expressions with multiple operations. To this end, most programming languages come with their own rules regarding operator precedence, to ensure consistency and uniformity, while executing programs. For example, in the case of JavaScript, the assignment operator has one of the lowest precedence while expressions inside a grouping operator (( )) have the highest precedence, meaning that sub-expressions that are grouped inside a pair of parentheses will be evaluated before the rest of the expression.

Prefix and Postfix Expressions

Clearly, operator precedence is a set of rules which are necessary to avoid the confusion that results from reading an infix expression. This makes prior knowledge of operator precedence vital: if one does not have prior knowledge of operator precedence, one cannot correctly evaluate an expression. Is there a way to represent expressions that does not rely on operator precedence to be evaluated?

There are two alternatives to infix expressions: prefix and postfix expressions. In a prefix expression, the operator is written before the operands. Thus, the expression 2 * 3 + 4 would be expressed as + 4 * 2 3 This clarifies that the multiplication operation should be applied on 2 and 3 and their result should be added to 4. A prefix expression removes any ambiguity regarding the application of operators on operands. This removes the need for developing elaborate conventions or rules to dictate operator precedence.

Similar to a prefix expression, in a postfix expression, the operator is placed after the set of operands. Thus, the above expression would be expressed as: 2 3 * 4 +.

S-expressions

Given the advantages of prefix expressions over traditional infix expressions, some programming languages solely rely on them to write logic. Typically, in such programming languages, expressions are divided into one or more ‘parts’ or ‘blocks’. Each such part or block will be contained within a pair of parentheses. Such expressions are called s-expressions. Thus, s-expression is a special kind of prefix expression, where every operation is contained within a pair of parentheses. Much like arithmetic expressions, it is possible to have nested expressions in a single s-expression.

An s-expression essentially contains two building blocks: lists and atoms. An atom is the basic unit of the expression which is not divisible any further. Each atom is differentiated from another by the use of spaces. In the above examples, the numbers 2 3 and 4 are atoms. Other data-types, like strings and boolean values can also be an atom. A variable can also be an atom.

A List refers to each block or segment of an s-expression which is contained within a pair of parentheses. The first atom in the list signifies a function or an operator. Thus, if f represents a function and args represent its arguments, the syntax of a list can be represented as follows: (f arg1 arg2 ... argn). Following this syntax, a simple list would be (+ 1 2). A list can be nested inside another list. Thus, a list can be composed of one or more atoms and/or other lists.

Here’s a list of valid s-expressions:

Lisp

Lisp was the first programming language to follow this “fully parenthesized prefix notation” (s-expressions). Lisp, which is loosely derived from the term “List Processor”, was developed by John McCarthy in 1960. Thereafter, many flavors and dialects of Lisp have emerged. Of these, Common Lisp and Clojure are two of the most well-known dialects of Lisp.

Clojure is highly prevalent in modern times as seen in the latest Stackoverflow survey. It is a programming language built on top of Java which provides a Lisp syntax for writing programs. The dialect of Lisp for which this project is building an interpreter for, relies on part of the Clojure syntax.

Goal

The goal of this project is to write a tiny version of the Clojure REPL, which can perform certain basic mathematical operations.

REPL stands for read-eval-print-loop. It refers to an interactive programming environment, that takes an input from the user, evaluates it and prints the result. Once a result is printed, the environment goes back to the read state to accept fresh inputs from the user, thereby creating a loop. The shell prompt on Unix-based systems is like a REPL.

Scope

The project will evaluate valid s-expressions. If expressions are incomplete (eg., unclosed parenthesis) or if they are not written as per the syntax of an s-expression, an appropriate error message will be displayed.

For the sake of simplicity, the project supports only basic mathematical operations, namely, multiplication, division, addition and subtraction. Thus, any s-expression containing any of these operations will be treated as valid. However, if an expression contains any other operator, the entire expression will be treated as invalid.

The project also handles variables. To initialize a variable, the keyword def should be used. This keyword acts as an operator and accepts the following two arguments: name of the variable and its value. Here’s how variables can be initialized: (def nameOfVariable 9). The same variable can be re-initialized with a new value in a single s-expression. Further, during a REPL session, once a variable has been initialized in one s-expression, it can be re-used in subsequent s-expressions.

An s-expression may contain two disjointed s-expressions, such that there is more than one resultant value at the end of evaluation. For example, in the following expression, (+ 7 8) (* 1 10), there are two values: 15 and 10. The project is implemented to only display the right-most result. In the above example, 10 will be displayed.

Running the Project

To run the code of this project, this Github Repository will need to be cloned:

git clone git@github.com:oitee/crisp.git

The necessary dependencies to run the project needs to be installed:

npm install

To run the project (Node.js needs to be installed):

npm run repl

Demo

Here’s a live in-browser demo of the project, compiled from Node.js using webpack and babel:

Implementation details

How expressions are read

The aim is to convert the input string (containing a sequence of characters) into a tree that expressly sets out the structure for evaluating each list in a valid expression. This is called LR parsing. To do this, the input string is read from left-to-right, without ever going back.

While traversing through each character in an expression, each collection of characters forming an atom is grouped together. This can be achieved as spaces demarcate atoms from one another. Also, a closing parenthesis implies the end of an atom (as it is not mandatory to use a space between an operand and closing parenthesis).

When an atom is parsed, it will be pushed to a stack. Once all the atoms of a list have been parsed and the list is complete, all the atoms belonging to that list will be popped from the stack. As every list is enclosed between a pair of parentheses, whenever a closing parenthesis is detected (while going from left-to-right of the input string), it would imply the end of a list. Thus, when a ) is detected, all the atoms pushed to the stack (thus far) will be popped out of the stack. As only the atoms of the current list should be popped, the popping should stop the moment a ( is popped. This would signify the beginning of the current list.

Once all the atoms of a list are popped, the list is evaluated. This is done by passing the collection of atoms comprising the list to an evaluator function. This function will first interpret the meaning of each atom. For example, if an atom contains digits, it will call the appropriate function to convert that atom into an integer. Similarly, it will convert the operator symbol to its corresponding function. Once this process is complete, it will call the relevant operator function and pass the set of operands belonging to the current list. The return value will be pushed back into the stack.

In this way, a syntax tree will be created incrementally and from bottom-up. For example, if the input expression is (* 1 (* 5 6) (+ 7 8 9) 10) , the atoms and lists will be built as follows:

First, the * operator will be pushed to the stack, along with the opening parenthesis (. Then, the following atoms will be pushed: 1 ( * 5 and 6. (For the sake of simplicity, the parentheses are not shown on the syntax tree).

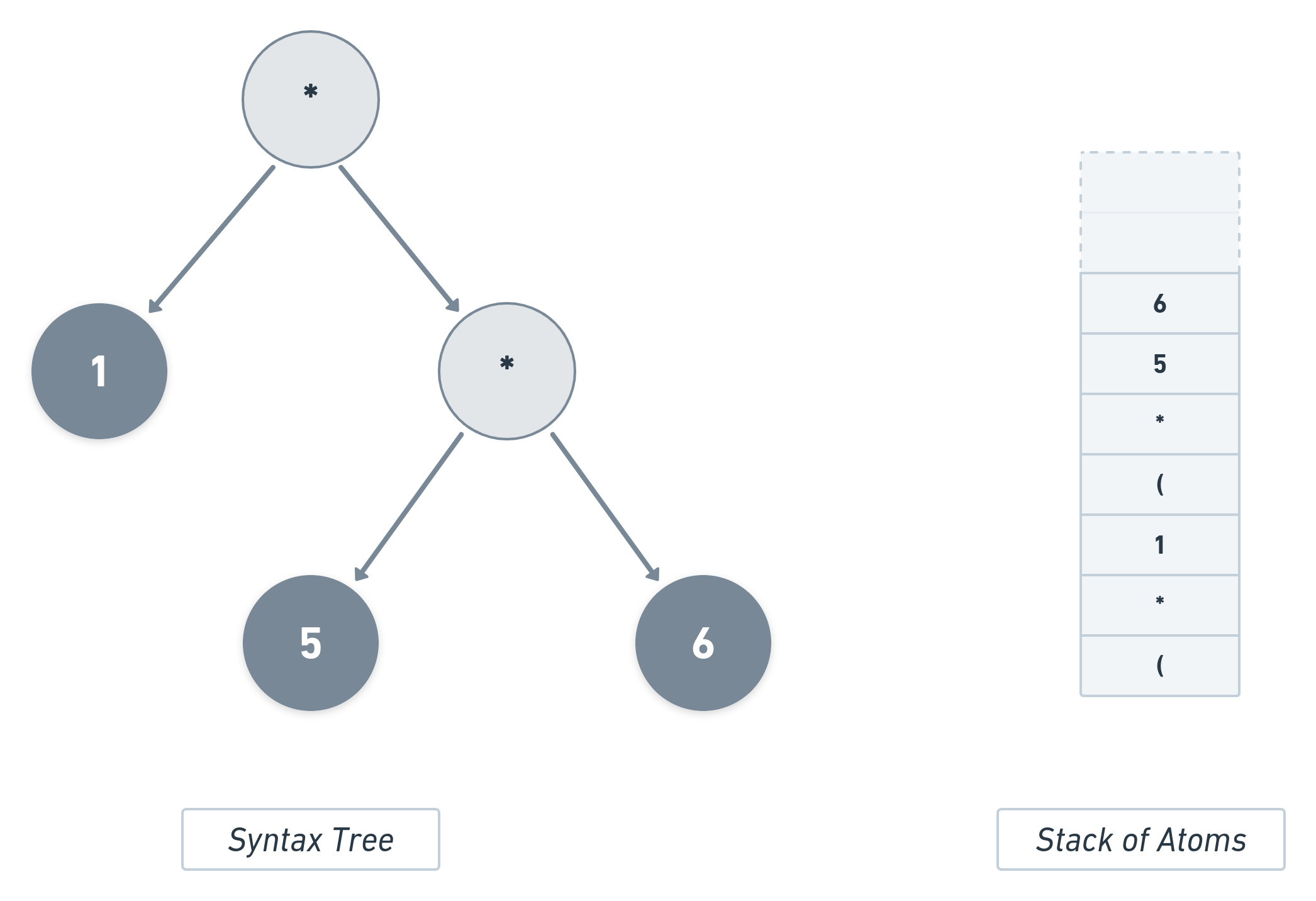
Now that there is a ), it will signify the end of the current list. So, all the atoms of the present list will be popped, namely 6 5 * and (. In place of these atoms, the value of (* 5 6) will be pushed into the stack. The syntax tree would now look like this:

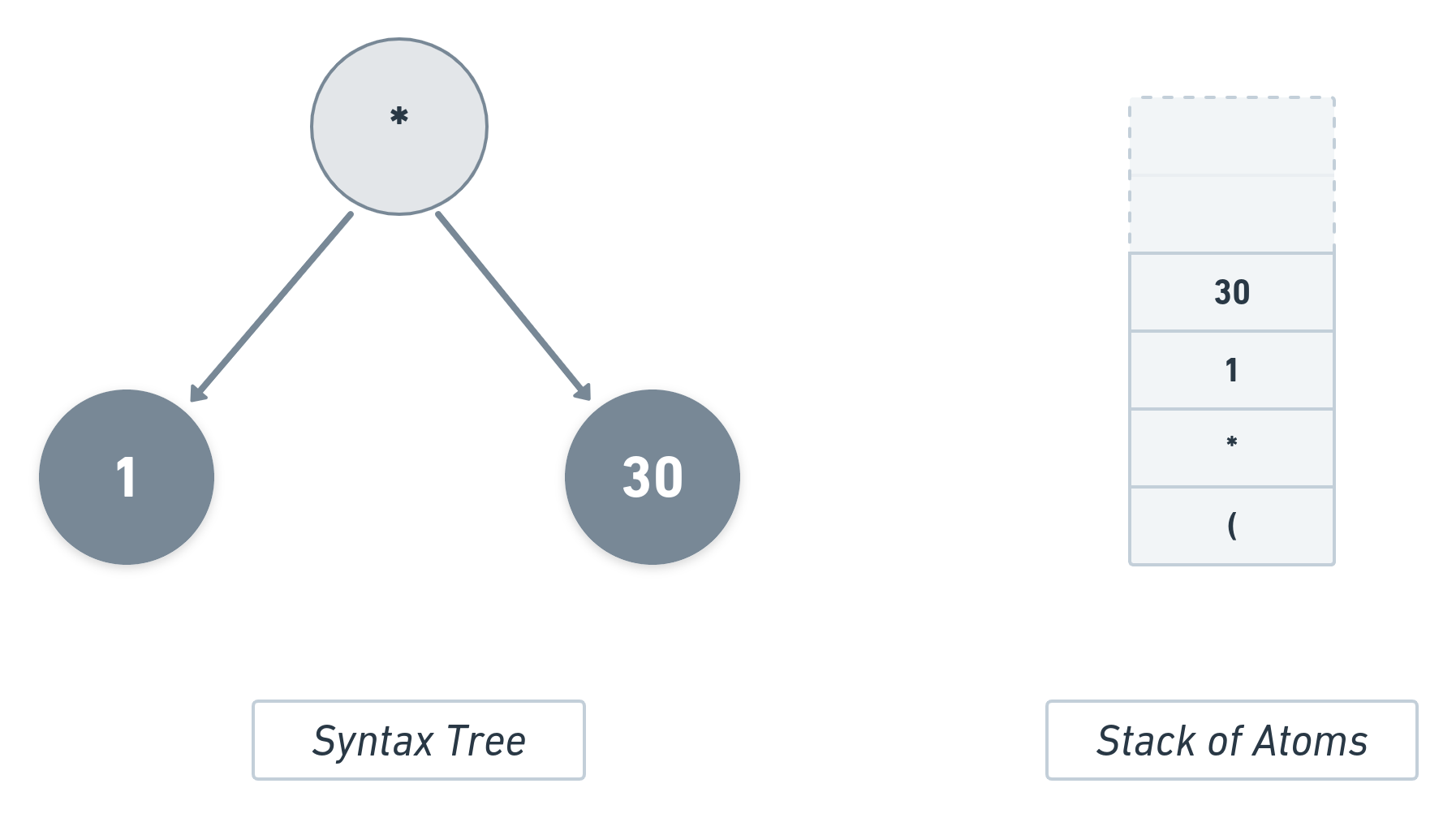
In a similar manner, the next set of atoms will be pushed, i.e., ( + 7 8 9 will be pushed:

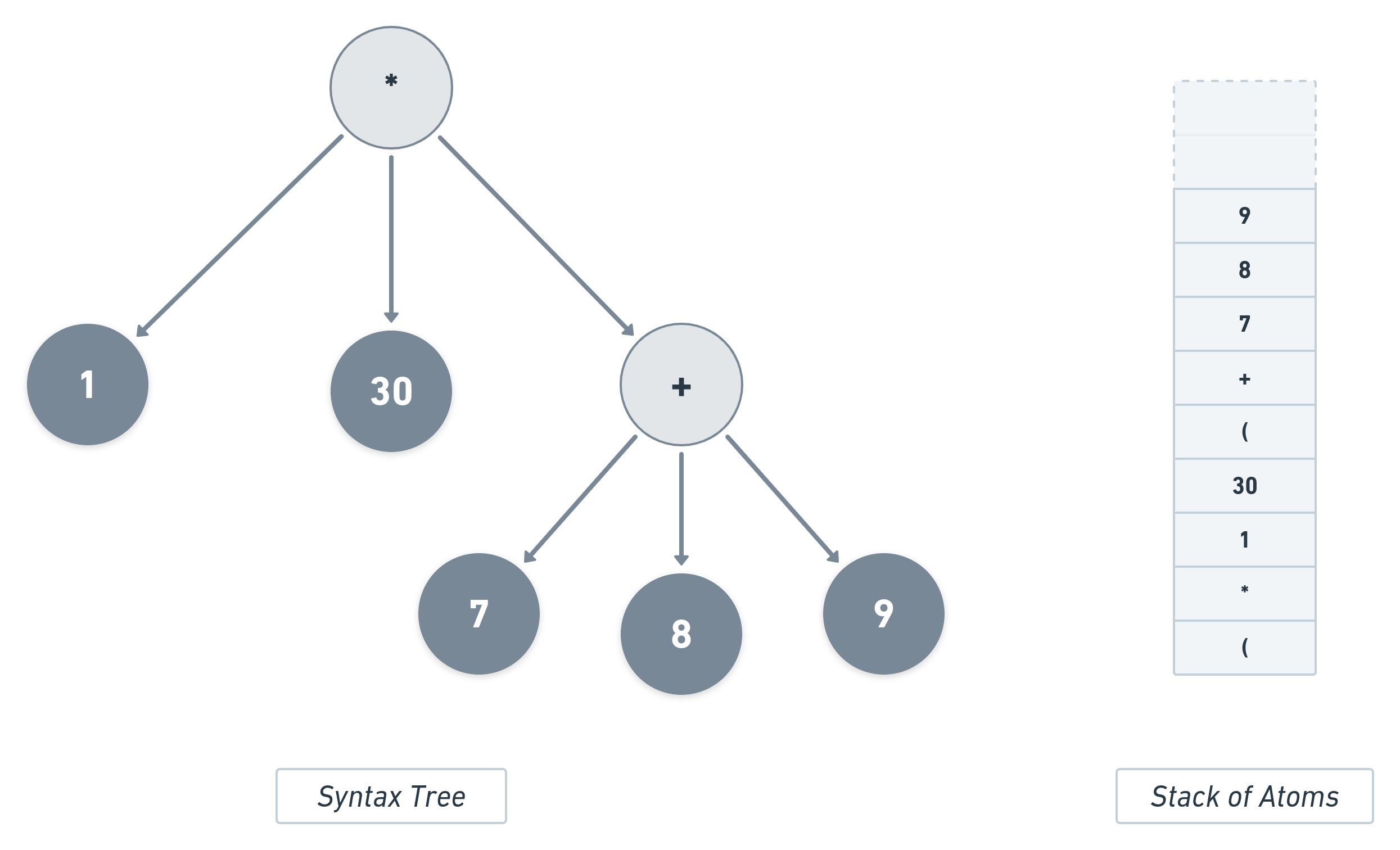
Again, the presence of ) would signify the end of the current list. So, all the atoms of this list will be popped and their result will be pushed into the stack. Finally, the penultimate atom, 10 will be pushed and then all the remaining values in the stack will be passed to the multiplication operator along with 1.

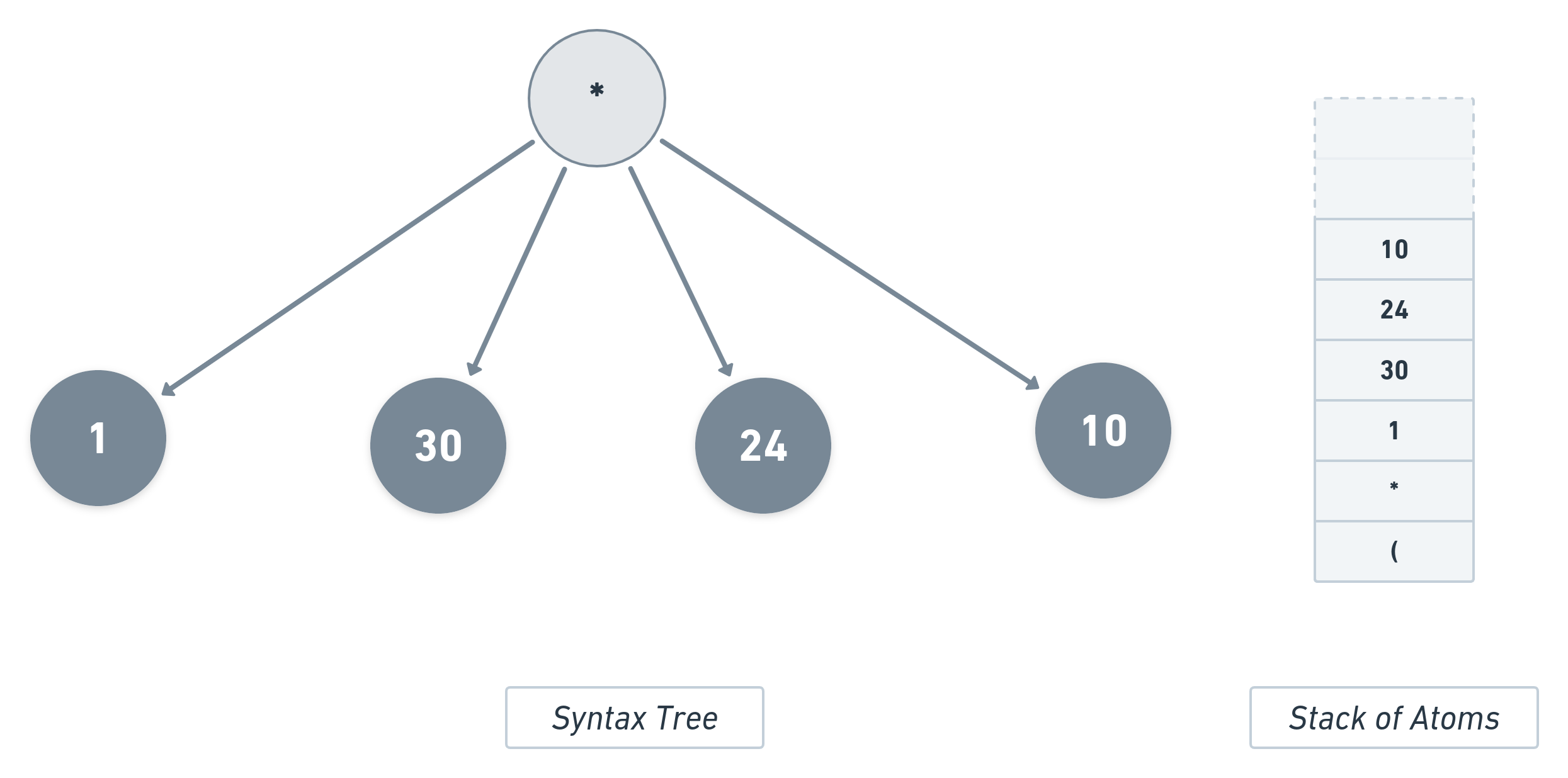
Now that there is no other element left in the expression, the return value of this function call will be the final output, i.e., 7200.

System Design

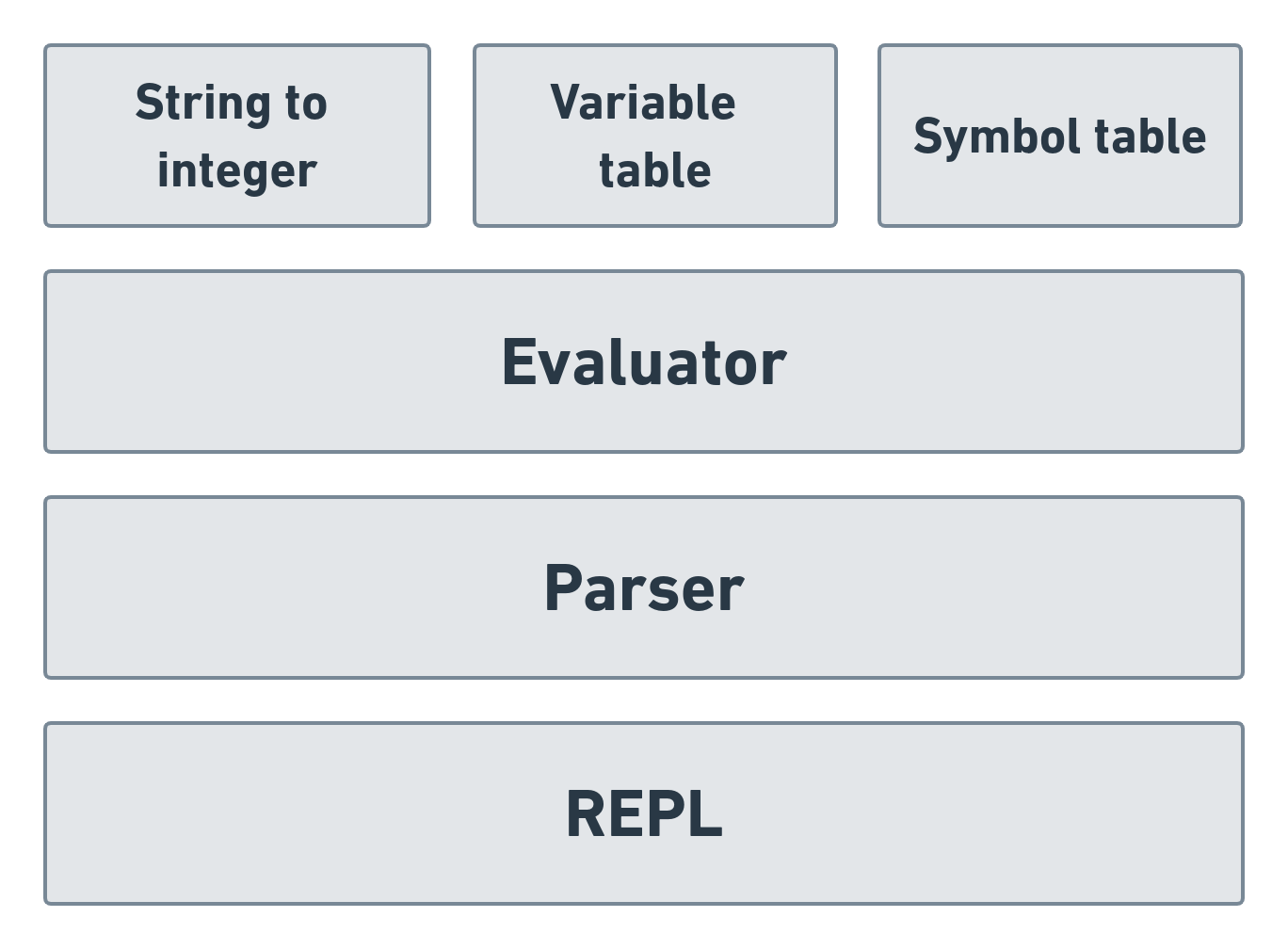
The project can be divided into three main components:

REPL: REPL runs the interactive environment. It accepts inputs from the user, passes it to the parser component and displays the final result, once it is generated.

Parser: The parser component parses each atom from the input string, by going from left-to-right. Each atom is stored in a stack data-structure. Once a list is formed, it transfers all the atoms of that list from the stack to the evaluator component. The value generated by the evaluator is pushed into the stack.

Evaluator: The evaluator component receives all the atoms of each list in the input expression. It checks if any of the atoms contains any digits and converts them into integers, accordingly. It converts the operator symbols and intialised variables to their respective values. Once each atom in a list has been tokenized, it evaluates the list expression and returns the result.

Further Improvements

Lisps are vast and have many features that are not implemented in this tiny project. The goal was to have a first version of a Lisp interpreter that could do the basic operations. Some of the main missing features that could be the first to be added to this are:

• Local scoping: While the project supports initialization and re-initialization of variables, it does not support initialization of local variables, within a given scope. For example, in Clojure, the keyword let allows for initialization of local variables within a given lexical context. The project does not support this feature.

• User defined functions: The project does not support function parsing. The program is built only to execute predefined operators. There is no scope to add new operators.

The project is hosted on this GitHub repository. Pull requests for the above improvements (or anything else) would be highly appreciated!