Linked Lists and Arrays

July 27, 2021

In this post, I attempt to understand two of the simplest data structures: arrays and linked lists. But before that, I try to see what a ‘data structure’ actually means.

What is a data structure?

Broadly, a data structure is a mere collection of data objects or items. More precisely, it refers to the manner of organising, modifying and storing data in a program.

Different programs need to carry out different kinds of operations. Given the operation to be carried out, we create the requisite data structure that is most suitable for that task. In some programs, the most significant operation may be to search whether a particular data value exists in a data-set. An array may be well-suited for such a program (as discussed below). While in some other program, we may need to conduct more complicated tasks, that may require more sophisticated data structures than simple arrays. Thus, keeping an eye on the nature of operations to be carried out, data structures are designed accordingly, such that those operations can be completed most efficiently. Thus, we design data structures to serve the needs of the algorithm at hand. In other words, “Algorithms + Data Structures = Programs“.

Unfortunately, there is no silver bullet when it comes to data structures: we cannot design a data structure that is universally efficient regardless of the algorithm at hand. Each kind of data structure provides certain benefits and guarantees, and have other draw-backs.

Arrays and Linked lists

Two of the simplest types of data structures are arrays and linked lists. Arrays contiguously stored values. Conceptually, an array is a collection of sequentially arranged data values, that are placed on a specific range of indices or positions. Arrays start from the index of 0 and proceeds incrementally. As arrays come built-in with most programming languages, we do not have to write constructors for arrays. Typically, arrays also have a fixed size (as discussed below) and their contents can be accessed by referring to their position or index within the array.

Linked lists are linear data structures, which are not contiguously arranged; instead, each unit, called a ‘node’, is connected to another unit, by way of pointers. A node of a linked list may be placed anywhere in memory, but each node will point to the next node and that node will point to the node thereafter and so on. By way of analogy, the pages containing search results of a search engine act like a linked list: the user can only go to either the next or the previous page from a specific page.

As linked lists can be created from scratch, it gives us freedom to design linked lists, which are best suited to the need at hand. A linked list in which each node carries a pointer to only the next or the previous node in the list, is called a singly-linked list. Most commonly, singly linked-lists (also called chains) will start with a head node, with each node pointing to the next node, and the last node pointing to null.

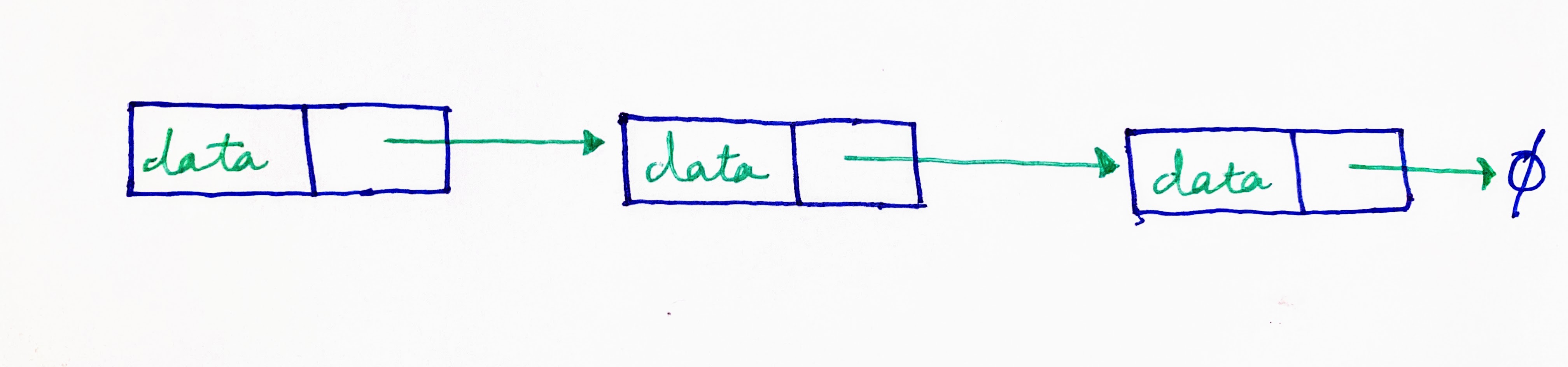
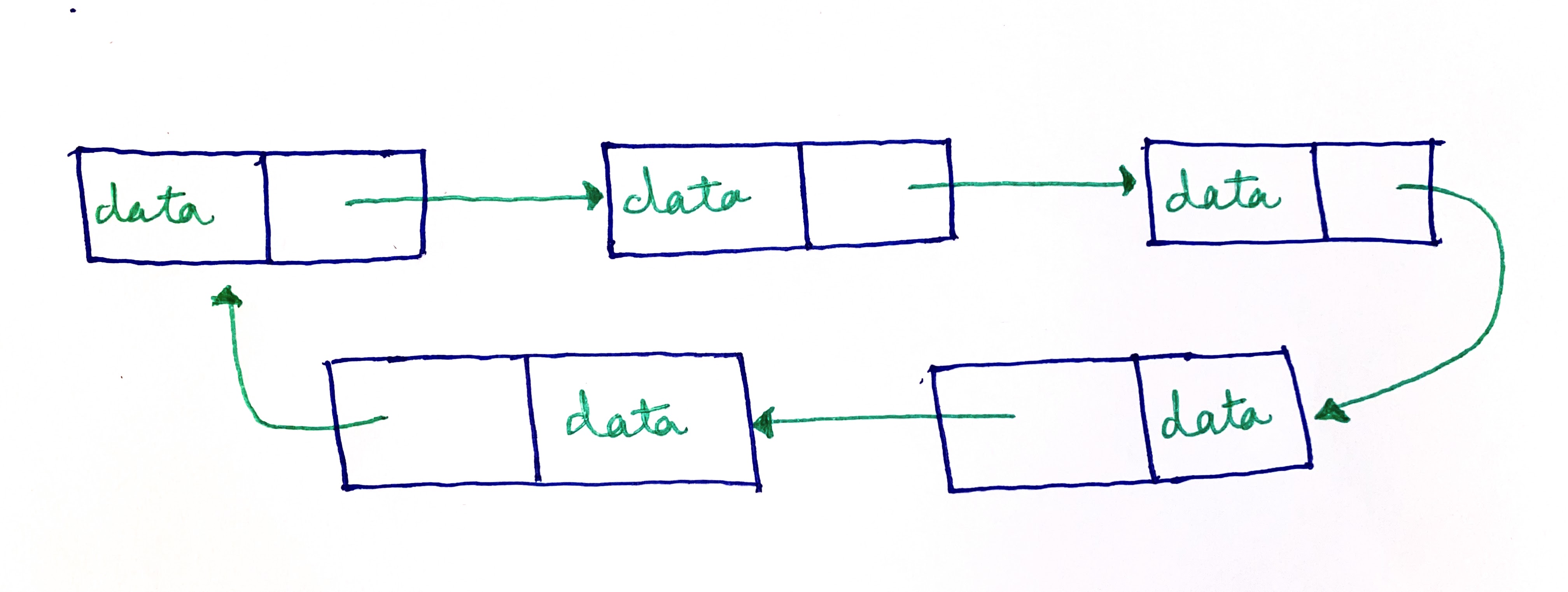
When the last node, instead, points to the head node, it will be called a circular linked list:

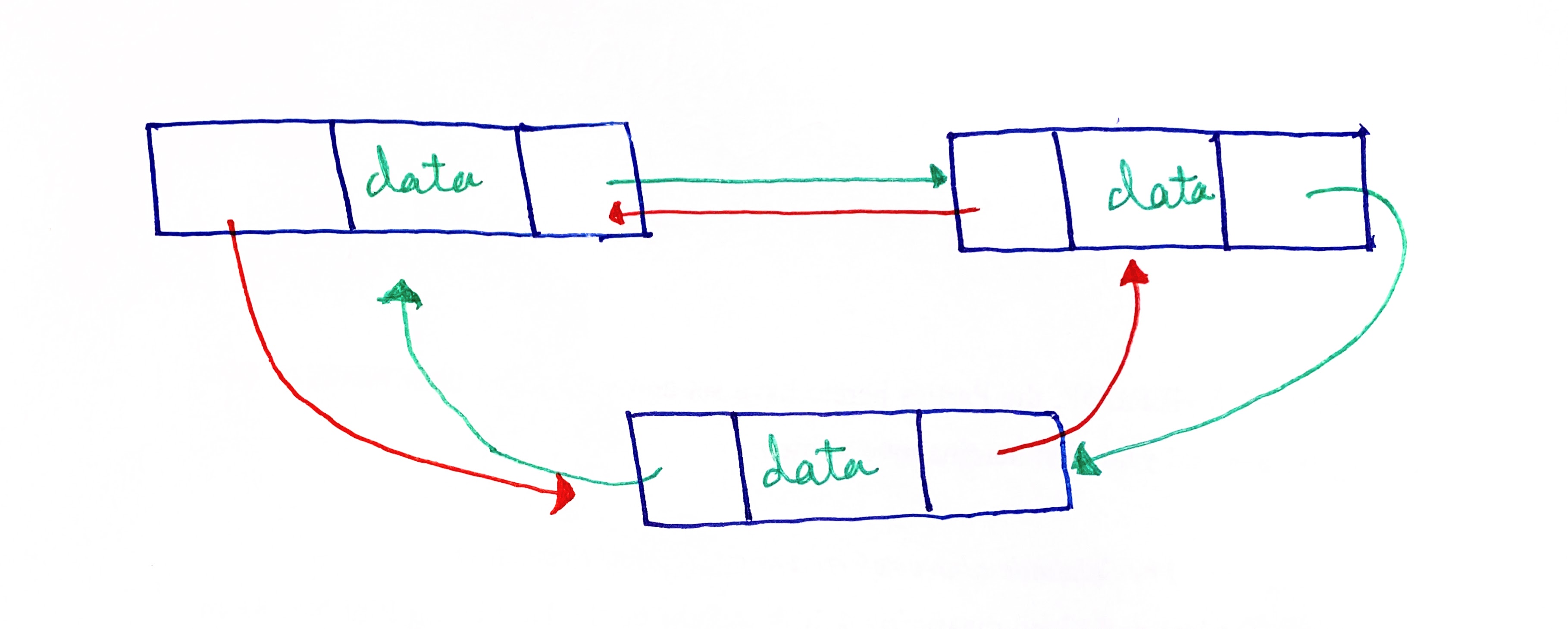
Nodes can also carry pointers to both the next and the previous nodes. Such linked lists are called doubly-linked lists. A doubly-linked circular list will have the head node pointing to the second node in the list, while also pointing to the last node in the list. Equally, the last node will have two pointers: one pointed to the penultimate node and the other to the head node.

Space Efficiency

Arrays need to contain only the data-items stored within them. However, in the case of linked lists, each node has to also carry a pointer to the next node. Thus, to store the same number of data-items, a linked list will need greater amount of space in the computer’s memory, for each node. In this regard, linked lists have an overhead, in comparison with arrays.

However, it is relatively difficult to insert additional items to an array, beyond its fixed allocated size. In other words, it is relatively difficult to add a new element to an array that was created to carry n items and that already contains n item. This is because arrays are contiguously arranged data structures, where each item is placed next to each other on the computer’s memory. Thus, in an array of length n, if we want to add a new element, we have to see if the memory address right after that array is already occupied or not. If yes, it would be very costly to add the (n+1)th item: a new memory location needs to be identified, for containing an array of (n+1) items. Then, all the existing items of the array will need to be copied to the new location and the older memory location will have to be freed. Finally, we can add the (n+1)th item. This may potentially keep happening each time we want to insert newer items to that same array (as we will keep hitting the fixed storage allocated for that array). As all of this happens in the background while working on a programming language like JavaScript, it may feel trivial when writing simple programs. But this may severely impact the efficiency of programs dealing with bigger data-sets, where the cost of copying existing arrays to a new location may lead to severe bottle-necks.

Also, in other programming languages, such as C, all of this does not happen in the background. The programmer has to manually request the computer to allocate a bigger memory space when an array reaches its initially allocated capacity. One common work-around while working in such programming languages is to create dynamic arrays, such that each time an array reaches its full capacity (of containing n items), the programmer will request for a memory allocation of 2n items, and then copy the exiting items to the first half of the new memory location. Again, when the array reaches its full capacity, a capacity to store 2*2n items will be requested and so on. This saves the trouble of requesting allocation of a new memory location for the entire array, for each additional element.

While dynamic arrays attempt to reduce the number of times we need to seek a new memory location for inserting additional items, it is not a perfect solution. Also, it may lead a scenario where we are creating large arrays which unnecessarily ‘hold-up’ unused memory space. This could happen, for example, when the length of the array decreases in size subsequently. Thus, if the number of elements in the array subsequently decreases to (4n-m), the array would have an additional unused empty space for m items. Thus, arrays are not ideal when dealing with data that keep changing (i.e., for algorithms that require frequent insertions and deletions).

However, unlike arrays, insertions and deletions are relatively simpler, as discussed below. And, so long as there is additional space available anywhere in the computer’s memory, we will never reach a point where we reach the maximum storage capacity when dealing with linked lists.

Accessing, Deleting and Inserting

Accessing Data

Elements in an array can be accessed very efficiently, as they will always be contiguous to each other. Thus, accessing the value stored in a specific index i will require only one operation. As a practical utility of this feature, if the elements of an array are sorted, finding out elements with the minimum value, maximum value, and median value can be done by one operation each. Additionally, it is convenient to iterate through various elements of an array, as they will always be sequentially arranged. Thus, if we need to check if an element exists within an unsorted array, we can run a simple loop to do this operation.

Linked lists, on the other hand, are not very efficient when we need to access specific elements in the list. This is because, it is not permissible to jump to a specific node in the list, as only the (n-1)th node will know the location of the nth node (in the case of singly linked lists). Thus, if we need to know the value contained by the last item in a linked list, we will need to traverse through the entire list, to reach the last node (assuming we do not already have a pointer to the last item saved from a previous iteration).

Insertions

For inserting an element anywhere in a data structure, it is relatively less burdensome to do so in a linked list. In a linked list, we can create a new node, and add its pointer to the head node, such that the newly added node becomes the head node of the list. Thus, if we are dealing with an unsorted linked list, where it is of little significance where we insert a new node, we can insert a new node with a fixed number of operations, irrespective of the length of the list.

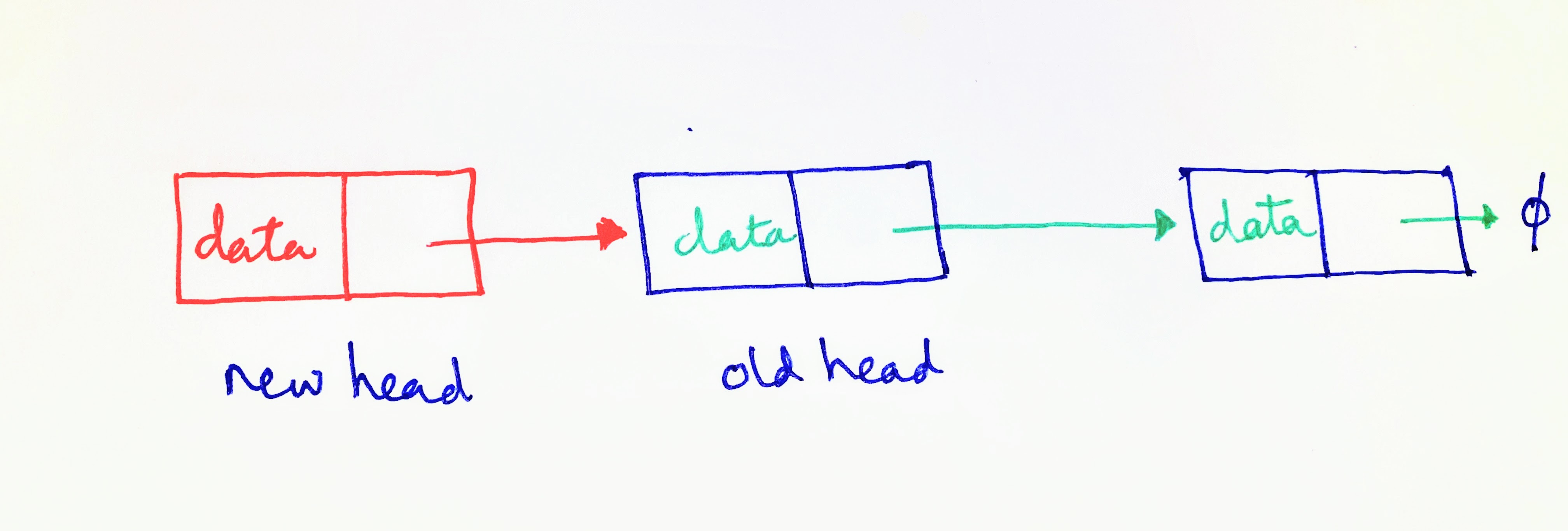
But this is not the case with an array. To insert an element in an array, we may need to shift the entire array to a new memory location, if the immediately next memory location after the size of the array is already taken up (as shown above). Alternatively, if we want to insert the new element at the beginning of the array, we will need to shift each element by one index. Thus, for insertions, arrays may not be the most optimal data structure.

Deletions

Just like insertions, it is relatively simpler to delete nodes in a linked list. Deletions can be executed by changing the pointer of the (n -1)th node to point to the (n + 1)th node, (instead of the nth node) thereby deleting the nth node from the list. Thus, if we have a pointer to the (n-1)th item, we can carry out deletions with a specific set of operations. For example, if we have to delete the head node in a linked list, we can do this by declaring the second node as the head node of the list. Similarly, if we have a pointer to the second-last node of a linked list, we can delete the last node, by changing the pointer of the second-last node to null .

However, if we do not have a direct pointer to (n-1)th node, we have to traverse through the entire list, starting with the head node, till we reach that node, and only then can we carry out the deletion operation.

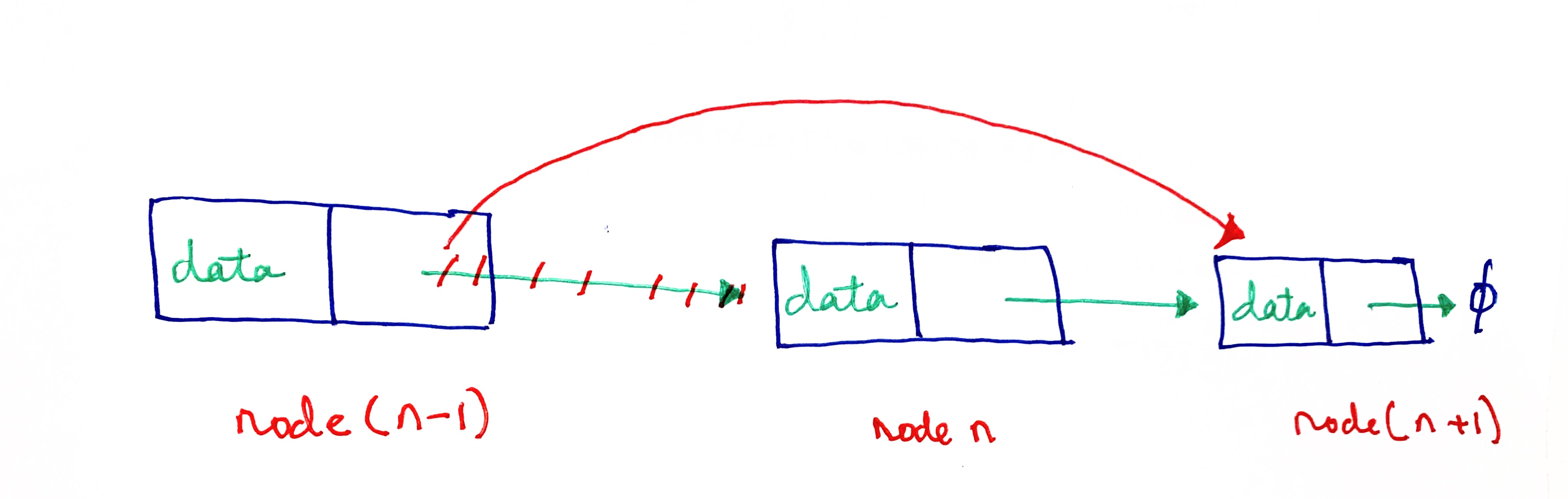
In the case of arrays, as noted above, if we delete any element, every element following that element will need to be brought-forward by one index.

Takeaways

From the above discussion, the following can be inferred:

• Arrays are better for random access of elements.

• But they have fixed size. Thus, insertions and deletions are costly.

• Linked lists take up greater space per unit than arrays, (as they have to store one or more pointers)

• But linked lists have dynamic size. So insertions and deletions are less burdensome.

In the next post, I will discuss how to create linked-lists in JavaScript.