Palindrome

July 20, 2021

In this post, I discuss my experience of solving my very first problem on LeetCode.

The Problem

To write a program that can check if an integer is a palindrome or not. It was also provided that negative integers and integers ending with one or more zeroes would be deemed to be non-palindromes.

It was suggested that the program be written without converting the integer to a string (though this was not mandatory).

My Attempt

I solved this problem using a for-loop:

var isPalindrome = function (x) {
  if (x < 0) {
    return false;
  }
  let lastDigit = x % 10;
  if (lastDigit == 0) {
    if (x == lastDigit) {
      return true;
    }
    return false;
  }
  let reverse = 0;

  for (let i = x; i > 0; i = Math.floor(i / 10)) {
    reverse = reverse * 10 + (i % 10);
  }
  if (reverse == x) {
    return true;
  }
  return false;
};

Is there a better way to solve this problem?

Although my solution was accepted by LeetCode, I was curious if there was a more elegant solution that took a lesser run-time or required lesser memory to do the same task. So, I looked into some of the solutions posted by others on the discussion section of LeetCode.

Taking a cue from some of the solutions, I figured a better way to write the same program. I realised that the key is to run the loop only till the half-way point.

When x is an even number

• First, we start with reverse = 0 , and x is the original value
• At each iteration, we increase reverse by the last digit in x
• At the same time, we reduce x by its last digit, as well
• Thus, at each iteration, reverse gains a digit and x loses a digit.
• During the course of the loop, there would be three stages, where x is a palindrome:
  • x > reverse
  • x == reverse
  • reverse > x
• Now, for non-palindromes, the second step will be skipped. In other words, when both x and reverse have the same number of digits , they will still be unequal.
• Given this, to determine the mid-point of the integer, we cannot rely on a condition where x == reverse (because not all xs will be palindromes). So we identify the mid-point by seeing when reverse becomes either greater than or equal to x
• Thus, the loop should run only when x > reverse, i.e., it will stop, the moment either x == reverse (in case of a palindrome) or x < reverse
• Once the loop is terminated, if reverse == x , then its a palindrome

When x is an odd number

• Even when x is an odd number, the same loop should be used. But note that in odd palindromes, the middle number is not repeated (eg. 12121).
• So, during the iteration of the loop, there will not come a time where the reverse and x will actually be equal to each other (even when x is a palindrome)
• Thus, the point for terminating the loop should be determined by seeing when x ceases to be greater than reverse. [In the case of odd numbers, this will happen when the reverse accumulates more digits than x, because there will never be a point when both reverse and x have the same number of digits]
• After the loop is terminated, to see whether x is a palindrome, we will need to ignore the middle number, and then compare the x and reverse.

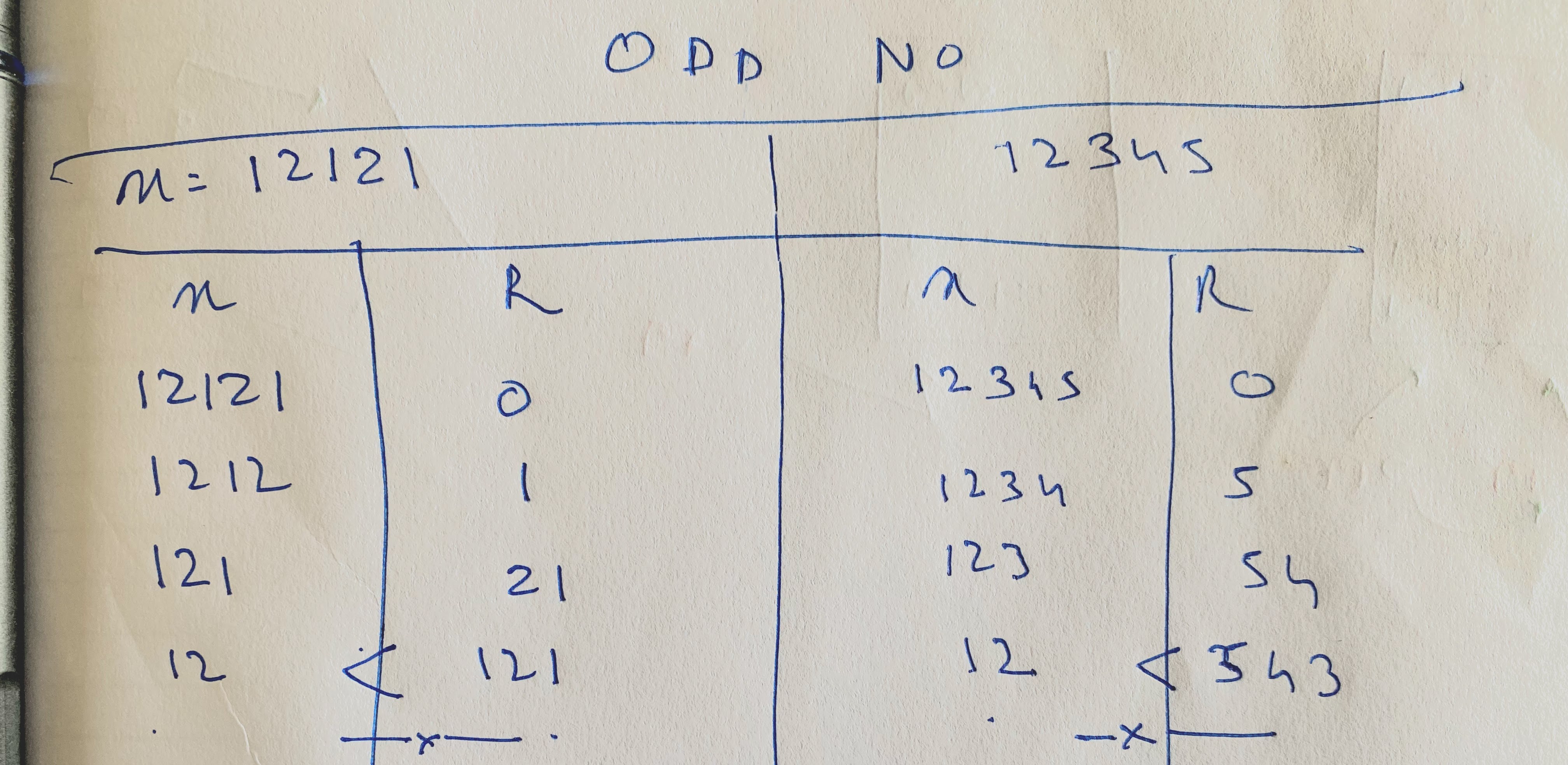
Comparing x with reverse

After the loop is terminated, we should see if x == reverse || x == Math.Floor(reverse/10), to see if x is in fact a palindrome. [In the case of an odd number, reverse will always have an extra digit (i.e., the middle digit). Thus, while comparing the two, we should see if reverse without its last digit equals to x].

Putting everything together:

let reverse = 0;
while (x > reverse) {
  reverse = reverse * 10 + (x % 10);
  x = Math.floor(x / 10);
}
if (reverse == x || Math.floor(reverse / 10) == x) {
  return true;
}
return false;
};