Implementing Graphs
A graph is an abstract data structure consisting of a set of vertices, each of which are connected to one or more other vertex. In this post, I explore this data-structure and implement some of its common operations.
What is a graph?
Graphs are powerful because they can be used to represent any form of relationship. For example, graphs can be used to represent road-systems in a city and relationships between different members on a social networking site.
Graphs and trees
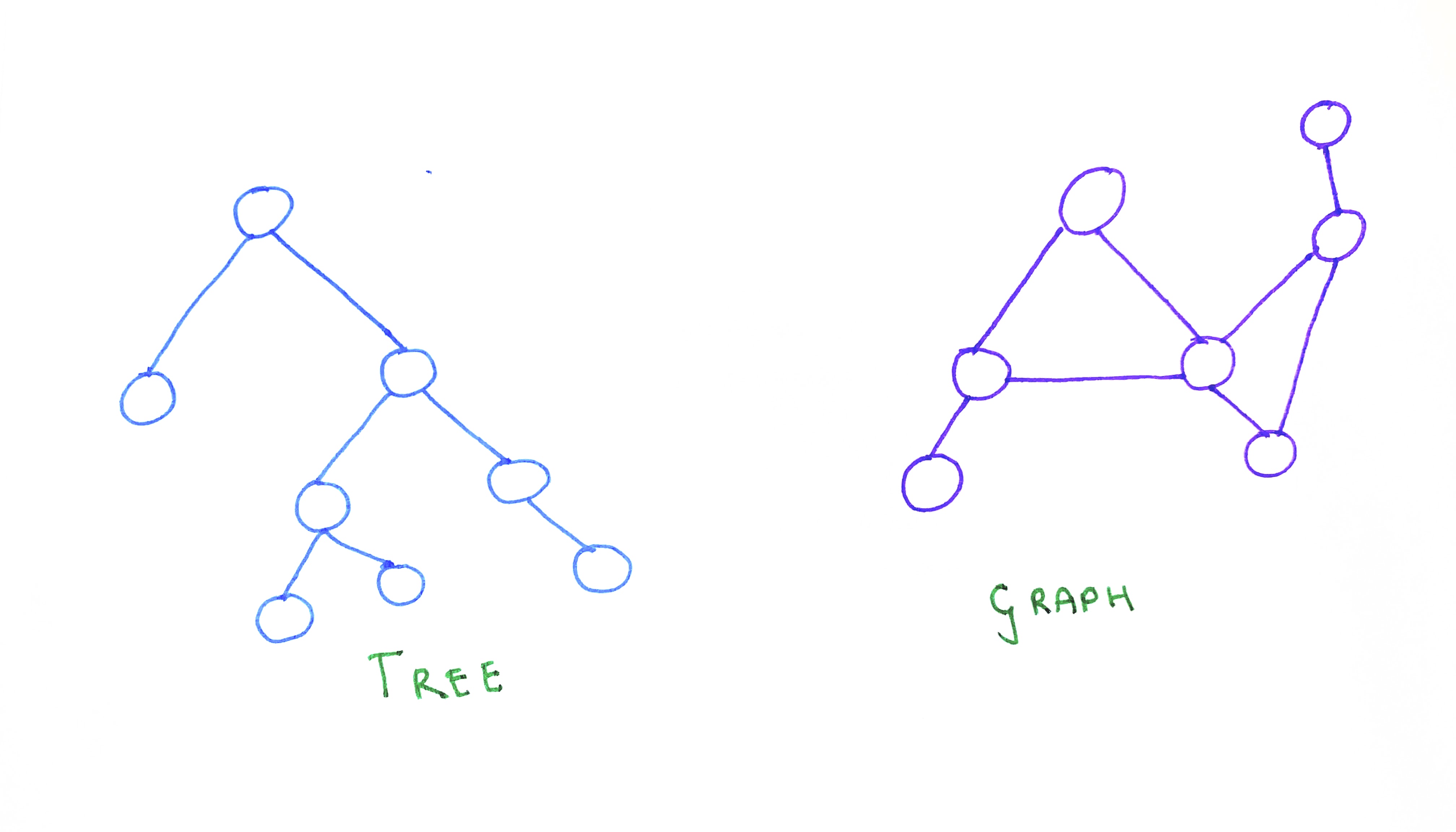
Trees represent hierarchical relations. They will always have a root which may have one or more sub-trees. A tree is, in fact, a special kind of graph. A tree is graph without cycles. To put it in another way, in a graph, it is permissible to connect any vertex (irrespective of where they are) to any other vertex in the same graph. As there is no specific restriction or order in which vertices need to be connected to each other, there can be multiple paths (also called ‘edges’) between two given vertices. But, in the case of a tree, each node will have only one specific route to reach another.
Directed and Undirected Graphs
Graphs can be directed or undirected. In a directed graph, between two neighbours, only one will contain a pointer to the other. It is akin to a one-way street. But in an undirected graph, each neighbour will carry pointers to all of its neighbours. Thus, between two neighbouring vertices A and B, A will contain a pointer to B and B will contain a pointer to A.
A graph is called a connected graph, if every pair of vertices is connected to each other by at least one path. Directed graphs will always be connected graphs. An undirected graph, however, can be a disconnected graph if there exists at least one pair of vertices that do not share a path between them.

Representing a graph
While writing programs, there are largely two ways of representing a graph:
- Adjacency matrix: A graph having n nodes can be represented in an n*n matrix, such that, if there exists a path between two vertices (say, i and j), the [i][j] cell will be
true, otherwise it will befalse. If its an undirected graph, both the [i][j] and the [j][i] cells will be marked astrue(orfalse, as the case may be). Instead of using boolean values, we can use0and1to represent the existence of a path. - Adjacency list: A graph can also be represented by maintaining an array for each vertex in that graph, such that, the array of each vertex stores a pointer to each of its immediate neighbouring vertices.
An adjacency matrix is relatively more efficient to represent graphs which have a dense network of paths. It allows for quick look-up and updation of new paths. But, it also takes up substantial space, especially when the number of paths is relatively low. For example, in a graph representing a social networking site, the total number of users (vertices) may be in the millions, while each user may have only a few hundred connections(paths). If we use an adjacency matrix to represent this graph, a substantial majority of the cells of the matrix will be empty.
An adjacency list is more useful to find out the degree (i.e., the number immediate neighbours) of a particular vertex. It takes up lesser space than an adjacency matrix. However, to insert a new edge or delete an existing one, it takes substantially more time than in an adjacency matrix.
Largely, adjacency lists are more convenient for programs dealing with sparse graphs (i.e., where the total number of vertices are comparatively greater than the total number of edges), while adjacency matrices are more useful for representing dense graphs. In this post, I will implement a graph using adjacency list.
Implementing a graph
As the case with most data structures, we need to first define a constructor function for a graph. As discussed above, the constructor function will need to create an array for each vertex, to store their adjacent vertices. Also, each vertex should store a specific value. The constructor can also contain a method, that can be called whenever we want to add a neighbour to a specific vertex. There can be another method, to first check if a specific vertex is already a neighbour of a given vertex.
class Graph {
constructor(data) {
this.data = data;
this.neighbors = [];
}
addNeighbors(...neighborVertices) {
for (let i = 0; i < neighborVertices.length; i++) {
if (!this.isNeighbor(neighborVertices[i])) {
this.neighbors.push(neighborVertices[i]);
}
}
}
isNeighbor(candidateNode) {
for (let i = 0; i < this.neighbors.length; i++) {
if (this.neighbors[i] === candidateNode) {
return true;
}
}
return false;
}
}
To create new vertices, we need to call the constructor Graph along with the new keyword. To add new neighbouring vertices to a given vertex, we need to add pointers to such vertices in the .addNeigbors method.
let a = new Graph("A");
let b = new Graph("B");
let c = new Graph("C");
let d = new Graph("D");
let x = new Graph("X");
a.addNeighbors(b, x, d);
b.addNeighbors(a, c, x);
c.addNeighbors(b, d);
d.addNeighbors(x, a, b, c);
x.addNeighbors(a, b, d);
Searching a Graph
Traversing through every vertex of a graph is one of the most significant operations involving a graph, as it is the only way to determine, for example, if a graph contains a specific value, or if a graph is cyclical etc.
There are two way to traverse through a graph, as explained below.
Depth-first Search
According to this method, we start with searching within a given vertex (which can be any arbitrarily chosen vertex, as it is not necessary to have a specific root node in a graph), and then visit any one of the neighbouring vertices of that vertex. Then, if that vertex has any neighbouring vertex, we visit any one such neighbour. We continue this, till we reach a vertex with no neighbours, that have not been visited already. Then, we trace back to the penultimate vertex, and visit another neighbour of that vertex. We continue this all the way upto the the first vertex. The traversal ends when either the specific value being searched for is found or till every single vertex has been scanned once. Thus, in a depth-first search, at the level of a given vertex, we will first recursively visit each neighbour’s neighbours, before moving on to other neighbours’s neighbours.
function dfs(vertex, visited = new Set()) {
console.log(vertex.data);
visited.add(vertex);
for (let i = 0; i < vertex.neighbors.length; i++) {
if (!visited.has(vertex.neighbors[i])) {
dfs(vertex.neighbors[i], visited);
}
}
}
In the above program, we first log the data contained in the vertex passed to the function dfs. Then, we run a for-loop to iterate through all the neighbours of that vertex. For each neighbour, we first check if it has already been visited. If not, we call the dfs function by passing that neighbour. The for-loop will terminate only after the dfs function is called for every un-visited vertex of the vertex that is passed to the function, during a given call.
As graphs can be potentially cyclical, it is very important to ensure that a vertex that is already visited, is not visited again. As otherwise, the search may never complete. To this end, Set object is maintained, called visited, which stores all the vertices that have already been visited.
In the case of binary search trees, we often implement a pre-order, a in-order, or post-order traversal. In each of these traversals, we visit the left sub-tree of a given node, before visiting its right-sub-tree. We do this recursively for each sub-tree within a tree. Thus, as we first go to the a neighbour’s neighbours (or, in the case of trees, children’s children) before visiting the other neighbours (or children), each of these traversals are examples of depth-first search.
Breadth-first search
According to this method, we first visit all the immediate neighbours of a given vertex, before moving on to the neighbours’ neighbouring vertices. To implement a breadth-first search, we can visit each neighbour of a given vertex in any order. Once every neighbour is visited, we can start visiting each of the neighbours of the first neighbour that was visited, in the same manner. In fact, the order of traversal during a breath-first search is very akin to the First-In-First-Out (FIFO) order. For this reason, queues are typically used to implement a breadth-first search.
function bfs(vertex) {
let q = [];
let visited = new Set();
q.push(vertex);
while (q.length != 0) {
let deq = q.shift();
if (!visited.has(deq)) {
console.log(deq.data);
visited.add(deq);
for (let i = 0; i < deq.neighbors.length; i++) {
q.push(deq.neighbors[i]);
}
}
}
}
In the above program, the array q is used to enqueue and dequeue each vertex and a Set object, visited, is used to store each vertex that has been visited once. Importantly, a neighbour of a particular vertex will be enqueued only if it has not been visited.
In the context of binary search trees, level-order traversals follow a breadth-first search, as each node’s neighbours (or children) are visited first before visiting their neighbours (or children).
Cloning a graph
If we need to clone an existing graph, we can use either of the two traversal methods, to visit every vertex of a given graph. To clone a graph, we will need to create identical copies of each vertices of the graph. Thus, each time we visit a vertex, we should create a new (cloned) vertex, and store the value and the neighbours of that vertex.
function cloneGraph(vertex, visited = new Set()) {
let q = [];
let deq;
let clonedVertex;
q.push(vertex);
while (q.length != 0) {
deq = q.shift();
if (!visited.has(deq)) {
clonedVertex = new Graph(deq.data);
clonedVertex.neighbors = deq.neighbors;
visited.add(deq);
for (let i = 0; i < deq.neighbors.length; i++) {
q.push(deq.neighbors[i]);
}
}
}
return deq;
}